Practical 5: Principal components analysis

Bert de Groot

Contents
Introduction
Principal components analysis of an MD simulation
Comparison to experimental structural data
References

Introduction

In practical 2, we've simulated the dynamics of a small protein. Although a protein's function is often intimately linked to its conformational dynamics, it is not always straightforward to extract the functionally relavant motions from a simulated trajectory. To illustrate this, we will focus today on the dynamics of a small, flexible protein: bacteriophage T4 lysozyme. Many organisms, including humans, have a form of lysozyme. It degrades polysaccharides (sugar molecules) that are part of bacterial cell walls and as such it has an antibacterial function. Click here for more background information on lysozyme. Download the structure of T4 lysozyme complexed to a substrate analog (PDB code 148L) from our site (it came from Protein Data Bank), and view the structure in pymol: 

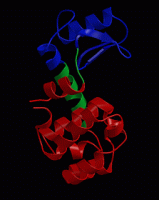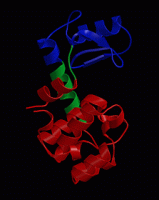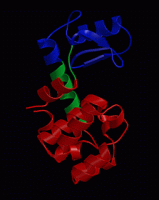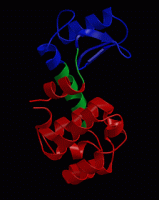
wget http://www3.mpibpc.mpg.de/groups/de_groot/compbio1/p4/148L.pdb
pymol 148L.pdb

highlight the substrate by typing (on the pymol prompt or in the grapics window): 

select sub,(resn NAG,MUB) 
color red,sub 
show sticks,sub

Now select the catalytic residues: 

select cat,(resi 11,20,26)
color yellow,cat
show sticks,cat

Now highlight the secondary structure: 

dss 
show cartoon

As you can see, the substrate is almost enclosed by the protein, with the active site (catalytic) residues buried in a groove on the protein surface.

Since it would take too long to calculate a long enough MD simulation during the course, we have prepared a simulation of the (substrate-free) enzyme. Now download this trajectory fragment and view it in pymol: 

wget http://www3.mpibpc.mpg.de/groups/de_groot/compbio1/p4/t4l.pdb
pymol t4l.pdb

Try out different visualisation modes in pymol to view as clearly as possible the structure and the dynamics of the protein. Use the same selections as above to highlight the catalytic residues and the secondary structure and press the "play" button at the bottom right of the main pymol window to see an animation of the simulation.

Question: Which motions can you identify? How can you imagine those motions to be crucial for the protein's function?


Go back to Contents

Principal components analysis of an MD simulation

Probably, you will appreciate the difficulty of identifying functionally relevant motions. One of the main reasons for this is that we see everything moving at the same time. Both local fluctuations and collective motions occur simultaneously, which makes it hard to distinguish the two types of motion from each other. A principal components analysis can help in such cases, as it can filter global, collective (often slow) motions from local, fast motions. Download the structure (ref.pdb) and the trajectory (md1_backbone.xtc). To reduce the size of the analysis, we will concentrate on the backbone only for the analysis. 

wget http://www3.mpibpc.mpg.de/groups/de_groot/compbio1/p4/ref.pdb
wget http://www3.mpibpc.mpg.de/groups/de_groot/compbio1/p4/md1_backbone.xtc

Now, have a look at the raw (backbone) trajectory: 

gmx trjconv -s ref.pdb -f md1_backbone.xtc -o md1.pdb -e 1000

(answer "0" when asked for a group). 

pymol md1.pdb

and press the "play" button at the bottom right of the main pymol window.
Now start the principal components analysis of this trajectory. This is done by building a so-called covariance matrix of the atomic fluctuations. Diagonalisation of this matrix yields a set of eigenvectors and eigenvalues, that describe collective modes of fluctuations of the protein. The eigenvectors corresponding to the largest eigenvalues are called "principal components", as they represent the largest-amplitude collective motions. 

gmx covar -s ref.pdb -f md1_backbone.xtc

and answer "0" twice when asked for a group. If you issue a 

ls -lrt

you'll see that gmx covar has generated both eigenvalues and eigenvectors, in files called eigenval.xvg and eigenvec.trr. View the eigenvalue spectrum with: 

xmgrace eigenval.xvg

The eigenvalues are sorted according to their size. As you can see, there are only a few large eigenvalues, all others are relatively small.

To more clearly see the eigenvalue distribution, we will select only the 30 largest eigenvalues.: 

gmx covar -s ref.pdb -f md1_backbone.xtc -o largest_eigenval.xvg -last 30
And visualize them: 

xmgrace largest_eigenval.xvg



To see what type of motion the indivudual eigenvectors correspond to, we filter the original trajectory and project out the part along a selected eigenvector: 

gmx anaeig -s ref.pdb -f md1_backbone.xtc -filt filter1.pdb -first 1 -last 1 -skip 100

to filter the trajectory along the first eigenvector. Answer "0" twice when asked for a group.

View the animation with: 

pymol filter1.pdb

Question: How would you describe this type of motion? How does it compare to the raw trajectory?

As you can see, the animation is kind of jerky. This is because the even such large-scale motions do not occur smoothly, but stochastically. To see a smooth animation of the motion along the first eigenvector, we can artificially interpolate between the extreme conformations sampled during the simulation along this eigenvector: 

gmx anaeig -s ref.pdb -f md1_backbone.xtc -extr extreme1.pdb -first 1 -last 1 -nframes 30

Answer "0" twice when asked for a group. View with: 

pymol extreme1.pdb

Now repeat the last two commands for the second eigenvector.

Question: How would you describe the motion along the first and second eigenvector? What happens with the substrate-binding cleft in these two motions?

To see the contrast with the other eigenvectors, now repeat the above procedure for eigenvector 15 (or 20, or any other number of your choice).

Question: The backbone of T4 lysozyme contains 486 atoms (162 residues and 3 backbone atoms per residue). How many eigenvectors/values would you expect? How many eigenvalues should be exactly zero, and why? How many should be approximately zero?

For a more quantitatve analysis, we can project the trajectory onto individual eigenvectors, and display the projections as a function of time: 

gmx anaeig -s ref.pdb -f md1_backbone.xtc -proj -first 1 -last 6
xmgrace -nxy proj.xvg

Question: Which eigenvector displays the slowest motion? Would you consider the simulation long enough to have sampled all relevant configurations? (one criterion for this is that all sub-conformations should have been visited multiple times).

Another way to visualise the sampled conformations in the subspace spanned by the eigenvectors is a so-called two-dimensional projection: 

gmx anaeig -s ref.pdb -f md1_backbone.xtc -2d -first 1 -last 2
xmgrace 2dproj.xvg

In this graph, each point represents a snapshot from the simulation, and the distribution shows the sampled region along the first two eigenvectors during the simulation.


Go back to Contents

Comparison to experimental structural data

We can use a PCA not only to analyse an MD simulation and extract the main concerted motions from a trajectory, but also for a comparison of multiple simulations or for the comparison to an ensemble of experimental structures, in terms of dominant, collective motions. For T4 lysozyme, a large number of x-ray structures has been determined (if you search the PDB for "T4 lysozyme", you'll find more than 400 structures). We have collected 38 non-redundant x-ray structures of T4 lysozyme, which are all together collected in allpdb_bb.xtc. Just like on the simulated trajectory, we can perform a PCA on the collection of experimental structures: 

wget http://www3.mpibpc.mpg.de/groups/de_groot/compbio1/p4/allpdb_bb.xtc
gmx covar -s ref.pdb -f allpdb_bb.xtc -nopbc

Now project the ensemble onto the first two eigenvectors. 

gmx anaeig -s ref.pdb -f allpdb_bb.xtc -extr extreme1_xray.pdb -first 1 -last 1 -nframes 30
gmx anaeig -s ref.pdb -f allpdb_bb.xtc -extr extreme2_xray.pdb -first 2 -last 2 -nframes 30

Again, choose "0" twice when asked for a group.

Question: What kind of motion is represented by the first and second eigenvector? How does this compare to the results from the simulation?

For a quantitative comparison of the simulation and the experimental strutures, we'll project both the experimental structures and the simulated structures onto the eigenvectors extracted from the x-ray structures: 

gmx anaeig -s ref.pdb -f md1_backbone.xtc -2d md_2d.xvg -first 1 -last 2
gmx anaeig -s ref.pdb -f allpdb_bb.xtc  -2d xray_2d.xvg -first 1 -last 2
xmgrace md_2d.xvg xray_2d.xvg

You now see the MD simulation in black and the x-ray structures in red. Since the x-ray structures are independent structures, it is confusing to have them connected by lines, which suggests a continuous path between them. In xmgrace, double click on one of the data points inside the plot, select the second set (G0.S1), under 'line properties', select 'none', and under 'symbol properties', select 'circle', and press 'Accept'. As you will have seen, eigenvector 1 of the x-ray ensemble describes an opening motion similar to the animation on the top-right of this screen, whereas the second eigenvector describes a twisting motion of both domains with respect to each other.

Question: How do the x-ray and MD ensemble compare to each other? Why do you think the MD simulation does not sample the x-ray configurations on the extreme left of the plot (the most open x-ray conformations)? And why do you think the twisting mode is sampled with a larger amplitude in the simulation than in the ensemble of x-ray structures?

Two additional simulations are available for T4 lysozyme, that started from different x-ray structures. Download the two backbone trajectories to your local disk: md2_backbone.xtc and md3_backbone.xtc. Cross project also these two trajectories onto the x-ray eigenvectors and visualise all three simulations and the ensemble of x-ray structures projected onto the first two eigenvectors of the x-ray ensemble. 

wget http://www3.mpibpc.mpg.de/groups/de_groot/compbio1/p4/md2_backbone.xtc
wget http://www3.mpibpc.mpg.de/groups/de_groot/compbio1/p4/md3_backbone.xtc
gmx anaeig -s ref.pdb -f md2_backbone.xtc -2d md_2_2d.xvg -first 1 -last 2
gmx anaeig -s ref.pdb -f md3_backbone.xtc -2d md_3_2d.xvg -first 1 -last 2
xmgrace md_2d.xvg xray_2d.xvg md_2_2d.xvg md_3_2d.xvg

Question: Which of the three simulations covers most of the crystallographic structures? Do you consider the simulations long enough to sample the most relevant conformations of the protein?

Question: All three simulations were of the substrate-free protein. Would you expect a more 'open' or a more 'closed' state as the most probable configuration in this situation?

Question: Alternatively, we could have carried out a Normal Modes analysis of this protein, approximating the energy landscape by a multidimensional harmonic energy minimum. Does the motion along the first PCA eigenvectors appear (quasi)-harmonic? If yes, which force-constant would you estimate? 

gmx anaeig -s ref.pdb -f md1_backbone.xtc -proj -first 1 -last 1
xmgrace proj.xvg

Optional

Think back of the first tutorial, where we simulated the noble gas Argon.

Question: For Argon in the gas phase (without periodic boundary conditions), what kind of results would you expect from a PCA analysis? Particularly, what would you expect the eigenvalue spectrum to look like?

Carry out a short simulation of Argon in the gas phase, using this topology, these starting coordinates, and these MD parameters. Now carry out a PCA over the Argon trajectory: 

wget http://www3.mpibpc.mpg.de/groups/de_groot/compbio1/p4/topol.top
wget http://www3.mpibpc.mpg.de/groups/de_groot/compbio1/p4/argon_gas.pdb
wget http://www3.mpibpc.mpg.de/groups/de_groot/compbio1/p4/md.mdp
gmx grompp -f md.mdp -c argon_gas.pdb
gmx mdrun -v

echo 0| gmx trjconv -f traj_comp.xtc -s topol.tpr -o nojump.xtc -pbc nojump 

echo 0| gmx covar -s argon_gas.pdb -f nojump.xtc -nofit -nopbc

Question: Is the eigenvalue spectrum as expected?

Have a look at the projections onto the principal eigenvectors with: 

gmx anaeig -s argon_gas.pdb -f nojump.xtc -proj -first 1 -last 6

and 

xmgrace proj.xvg

Question: Do you note the similarity of these projections to cosines? What implications does this have for protein trajectories, where the principal mode projections appear as cosines? answer.

Go back to Contents

Further references and advanced reading
For questions or feedback please contact Bert de Groot / bgroot@gwdg.de