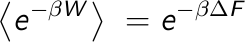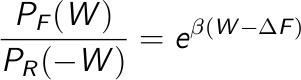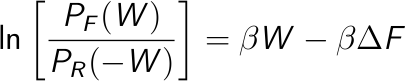Practical 10: Free energy calculations from non-equilibrium dynamics

Contents

A. Introduction

In a previous tutorial we learned two methods to compute Free Energies associated to a given thermodynamic process: the solvation Free Energy of sodium ions in water and the folding of a peptide in water. In the first case we used Free Energy Perturbation (FEP), that takes advantage of the fact that Free Energy is a state function. For an equilibrium process, the Free Energy is independent on the path the system takes to move from state A (no sodium in water) to state B (sodium fully solvated in water).


As the sodium-water interactions were slowly turned on, we recorded the changes in potential energy. Integration of these potential energy differences over the morphing path yields the Free Energy.
To study the themodynamics of peptide folding, we relied on the Boltzamn probability distribution of themodynamic ensembles in equilibrium. The relative population of folded and unfolded states was extracted from a molecular dynamics simulation, which gives direct access to Free Energy differences.

So far we have used equilibrium dynamics to compute Free Energies: the transition between states is done infinitely slow, or reasonably slow, and the work performed/gained is equal to the Free Energy. By extracting Free Energies from equilibrium simulations we have to make sure that the system fulfills a Boltzmann equilibrium. In practice this means that we have to sufficiently sample the phase space available. While this is conceptually not a problem, in practice this poses a problem for systems with many degrees of freedom and long relaxation times.

- The Jarzynski equation

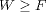 As a follow up, today we will learn that we can use non-equilibrium dynamics to compute Free Energies. Although several new relationships for non-equilibrium thermodynamics were found during last century, the link between the work and the Free Energy remained as an inequality: the work is always greater or equal to the underlying equilibrium Free Energy ( ). It was not until the very end of last century (1997-1998) that new expressions directly relating the work and the Free Energy were found. The first one, known as the Jarzynksi equation, relates the ensemble average over an exponential distribution of the work with the Free Energy.


This relationship turned out to be extremely useful, as it allows, for example, to compute binding Free Energies of ligands by repeteadly enforcing the unbinding and recording the work distribution. This process can be mimicked in a computer experiment, with the advantage that the simulation times are reduced due to the fast non-equilibrium trajectory. Nevertheless, several experiments have to be carried out to get a reasonable estimate of the work distribution.

- The Crooks theorem

 Yet another non-equilibrium relationship, even more fundamental, was put forward by Crooks in 1999. The expression is grounded on microscopic reversibility, and one useful theorem derived from it is the Transient Fluctuation Theorem (TFT). The former relates the ratio of the work distribution for a Markovian process that moves from state A to state B and from state B to a A with the dissipated work involved in the transformation. Look at the wikipedia page for more information, if you're interested.




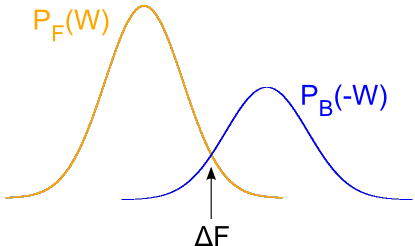
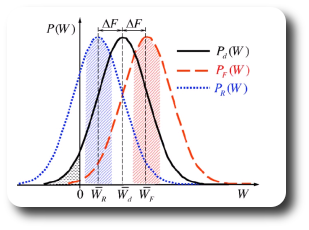
A first approach is to estimate the free energy as the work value W where both distributions overlap, PF(W) = PB(-W):




A second approach is to take the logarithm of the Crooks equation,




Then, plot the left side of this equation vs. the work, which is a straight line, and estimate the free energy from the intercept.

Today we will take advantage of these recent breakthroughs to compute Free Energies ( an equilibrium property ) from non-equilibrium processes. To illustrate the capabilities of these relationships we will first study the solvation Free Energy of an ion in water, now by means of several fast (non-equilibrium) Free Energy Perturbation simulations. A second application of non-equilibrium relationships will serve us to elucidate the Free Energy profile for an ion permeating through a peptidic ion channel.

Go back to Contents

B. Solvation free energy of a sodium ion in water using the Crooks theorem

This exercise uses the same simulation technique (FEP) previously introduced in these tutorials. We learned that sufficiently long simulations were needed to obtain a converged value for the solvation Free Energy, where the morphing parameter lambda was slowly changed from 0 (no ion-water interactions) to 1 (all interactions switched on).


Another way of computing the solvation Free Energy would be to perform multiple (fast) simulations. Some will drive the system from an equilibrated state A (lambda = 0) to a final state B (lambda = 1). We will call such a process the Forward transformation. Additionally, some will be perfomed in the opposite direction (Reverse transformation), e.g. an equilibrated system in the B state will be transformed into state A. By collecting the work performed in either Forward or Reverse transformation we can obtain their respective probability distributions. Recalling Crooks' Transient Fluctuation Theorem we know that the point where the two probability distributions meet the dissipative work is zero. Hence, at this point the work will equal the Free Energy.




For the exercise we will need a set of starting structures in the initial (no sodium-water interactions) and final state (all interactions present). Recall that while the interactions are not acting (state A), the ion is actually present in the simulation box. Additionally, we need a topology file describing the interactions in the system and a MD parameter file.

In this zipped folder you will find all the files needed for the exercise. Once you have donwloaded the file, use the following commands to extract its contents

tar -xvzf practicum_crooks.tar.gz ; rm -f practicum_crooks.tar.gz
or, if you downloaded to the default 'Desktop' folder:

tar -xvzf Desktop/practicum_crooks.tar.gz ; rm -f Desktop/practicum_crooks.tar.gz

Now move to the extracted directory:

cd practicum_crooks

There you will find one folder that contains the necessary files for the simulations in Forward direction and another one for the Reverse transformation. As a first approximation, we will compute one very fast FEP simulation in the forward direction. In this case the lenght of the simulation is just 10 ps. During this time the morphing parameter will be switched from 0 to 1 in increments of 0.0002. Let's go for it,

cd fast_FWD
Prepare the MD run by issuing

g_grompp -f forward.mdp -c fwd_snapshot.pdb -o fwd_run.tpr -p topol.top


Start the simulation like this,

g_mdrun -s fwd_run.tpr -v
The molecular dynamics program generates, as you know, a dhdl.xvg file that contains the dG/dlambda as a function of time. We will integrate the curve with respect to the time and finally divide by 10 (the simulation time), exactly as we did last practical.
Open the file with xmgrace

xmgrace dhdl.xvg
and under "Data", select "Transformations", followed by "Integration", and press "Accept". Remember that the result of the integration has to be divided by 10.

As you can see, the result is quite off the expected value, around -393 kJ/mol. As we know, this comes from the dissipative contributions that arises due to the fast morphing.
We know that if the obtained "Free Energy" would be a state function, the value for the Reverse transformation should be the same. Let's check it! Go to the folder were the input files for reverse FEP are located,

cd ../fast_REV
Here the initial state is the sodium ion fully hidrated in water. As before, we prepare the input file and run the simulation.

g_grompp -f back.mdp -c rev_snapshot.pdb -o rev_run.tpr -p topol.top



g_mdrun -s rev_run.tpr -v
Integrate the dhdl.xvg as we did before, remember to divide by 10!

As you can see, both results differ quite a bit. Since we performed the simulations too fast, the difference of the computed "Free Energies" is not zero, we apply/obtain work to/from the system.

Question: ... but what happens if we average the two results (Forward and Reverse)? Does the result get closer to the actual converged result for the Free Energy difference (around -393 kJ/mol)? Why does this happen?

A way to improve the results is to actually use Crooks' TFT. This demands getting a probability distribution for the work (our non-converged Free Energies) in the Forward (lambda 0->1) and Reverse (lambda 1->0) directions. It is important that the initial state of the system is in thermodynamic equilibrium. The initial structures you will use for the Forward and Reverse simulations were obtained from different snapshots of equilibrated simulations at lambda 0 and 1 respectively.
Since the method implies running many simulations in each direction, we will use a set of simple shell scripts (tiny programs that make life easier when dealing with repeated tasks). Don't worry if you don't really understand the syntax, the basic steps you already know: prepare input file based on structure, interaction parameters and MD input file.

We can start with the Forward runs.

cd ../FWD_RUN_TFT
You can see that there are several folders, each containing the inital structures. Let's create the input files (so called tpr files) for the simulation runs first.

For that open the file create_tpr.csh with your favorite text editor and modify the line:

grompp -f ../forward.mdp -c fwd_snapshot_$count.pdb -o fwd_$count.tpr -p ../topol.top

to

g_grompp -f ../forward.mdp -c fwd_snapshot_$count.pdb -o fwd_$count.tpr -p ../topol.top -maxwarn 1

We need to ignore the first warning that results from atom name mismatch due to the names of Sodium ions being dissimilar (Na vs NA).



Now open the file do_md.csh with your favorite text editor and modify the line:

mdrun -s *.tpr >& md.lis

to

g_mdrun -s *.tpr >& md.lis



From the FWD_RUN_TFT directory now execute

./create_tpr.csh
Now we can start the dynamics. The next command executes the script that takes care to start each simulation sequentially,

./do_md.csh
>>> ( Since it takes some time to compute each run, approx. 1 minute each, you can use the time to read the theory above and/or the introduction for next exercise ) <<<

If all went fine, we should have a dhdl.xvg file in each folder.

Estimation of the free energy as the intersection point of the forward and backwards work distributions

The next step will be to compute the work for every run and put the data in one file. Luckily you don't have to integrate every single dhdl.xvg file by hand. The next script takes care of it: it enters each folder, integrates the FEP file and even divides by the simulation time!

Please open the file "gather_work.csh" and modify the line:

../turbo_integration.csh dgdl.xvg | tail -n1 | awk '{print $2/10}'

to

../turbo_integration.csh dhdl.xvg | tail -n1 | awk '{print $2/10}'

Now, run it with:

./gather_work.csh
The command outputs the results to the screen. To write them directly in a file, say Work_fwd.txt, do the following,

./gather_work.csh | grep -v csh > ../Work_fwd.txt
Good, now will do the same but for the reverse simulations. To save the time required for the simulations. we have already done these for you, and we can now simply collect the result:

cd ../REV_RUN_TFT
./gather_work.csh | grep -v csh > ../Work_rev.txt
We now generated a series of possible work values for the forward and reverse FEP. Ideally, we would compute enough values to estimate a probability distribution of the work. If we don't have any extra information on the distribution function, it is necessary to have an overlap between the two distributions, since Crooks' TFT states that the work value that equals the true Free Energy is the one which has the same probability in the forward and in the reverse distribution.
We will generate histograms (or numerical estimates of unormalized probability distributions) for both work distributions with xmgrace,
Open them both directly with

cd ..
xmgrace Work_fwd.txt Work_rev.txt
To compute histograms, first of all create a new graph : go to "Edit" -> "Arrange Graphs" and set the "Cols" value to 2. Apply the changes and Close. Now you have two graphs. To compute the histograms, go to "Data" -> "Transformations" and click on "Histograms". From the "Source" list click now on the first (G0) and then the first "Set" (GO.SO). As a "Destination" list select the second (G1). Now have a look at the values you have for the distribution, typically between -420 to -360. Use these numbers as "Start at" and "Stop at" and something like 40 bins. The more data points, the more bins we could use. Click in "Normalize" and then press "Apply" to perform the histogram on the first data set. To obtain one for the second data set, simply select (G0.S1), under the second "Set" in the first graph in the "Source" list and press "Apply". In order to see the histograms, select the new graph by clicking it with the mouse and then press the "AS" (for Auto Scale) button on the upper left.

Question: Based on the two adjacent histograms, which is the estimate for the Free Energy value? How could we improve the estimate? Do you think that 10 data points can create a significant ensemble?
Let's try increasing the number of transitions. We have prepared 400 short 5 ps simulations for both the forward and the backwards transitions. You can download here all the output dhdl.xvg files.
First extract the contents of the folder and get in the extracted folder
tar -xzvf 400runs.tar.gz
cd 400runs/FWD_RUN_TFT
Now repeat the steps of the previous section to extract the work from each dhdl.xvg file, gather all work values into a txt file, and create the histograms for both the forward and reverse transitions.
Question: Which is the new estimate for the Free energy based on the intersection point of the distributions? How does this estimate compare to the previous calculations?

OPTIONAL: Estimation of the free energy taking the logarithm of the Crooks equation

Once you obtained the work distributions, it is possible to estimate the free energy taking the logarithm of the Crooks equation (see here ). You should extract the portion of both distributions in which there is an overlap and PF(W), PB(-W) are not zero (to avoid singularities). Then, plot ln ( PF(W) / PB(-W) ) as a function of W and do a linear regression. The slope of this curve is β = 1/KT and the intercept is -βΔ F

Questions: How much does the regression deviate from a straight line? How does the estimate of β = 1/KT compare with the input value, β = 1/(2.5 kJ/mol) , at the given temperature of 300 K? What is the estimate of the free energy? How does it compare with the previous estimations?

Go back to Contents

C. Potential of Mean Force for a potassium ion permeating an ion channel

Ion channels, located in the lipidic membrane that separates organelles or cell membranes, allow the passage of ions from one side of the membrane to the other. Their structure and composition is diverse, although they share some characteristics. Gramicidin is a small peptidic ion channel of 30 aminoacids, whereas potassium ion channels, like KcsA, are proteins with quaternary structure. Their function afftects electrochemical gradients, and thus ion channels have a fundamental role in the bioenergetics of living cells. A subtle balance of ion gradients is, for example, responsible for the polarization-depolarization of neuron's membrane that leads to electrical signal transmission in nerve cells. Many membrane proteins need to couple their transport mechanisms to ion gradients. For these and many other reasons, ion channels are of great interest in biophysics and electrophysiology, as well as in medicine.


Ion channels differ from ion transporters because they do not need and external energy source to achieve their functionality. Their activity can be gated by several means: voltage gated, drug binding, pressure, or simple ion gradient.
Most ion channels present a selectivity filter to achieve specificity for certain types of ions. These regions are usually carefully constructed to have favorable stabilizing environment for the ion they want to permeate. Ions in solution are stabilized by the interactions with the solvation water shell, as we saw in the previous exercise. As the ion enters the channel several interactions with solvating waters disappear, which can not be fully compensated by the channel's partially hydrophobic interior. Since ions are charged species, this desolvating effect is much stronger than for water, and so the ion flux is significantly lower compared to water flux.

Molecular dynamics is a very powerful tool to study the energetics of ion channels, provided a good set of parameters that describes the interactions between channel, ions and membrane. Nevertheless, the high activation energy for ion permeation makes direct estimation of ion flux almost impossible: the simulation time needed to observe a significant amount of ion translocations is currently out of reach. Luckily, rate theory provides a clear connection between the underlying energetics for ion permeation and their rates or fluxes. Several theories and methodologies exist that connect the Free Energy profile, or Potential of Mean Force, with rates. Although they vary in the level of sophistication, the main idea is that the flux is propotional to the ratio of populations in the lower energy state and the population in the highest energy along the path. Since the populations in steady state are Boltzman weighted, the flux is inversely proportional to the exponential of the activation energy, the difference in energy between the lowest and highest energy along the path.



In order to predict ion selectivity, or compare ion fluxes qualitatively, we can then extract the Potential of Mean Force for the desired ion permeation and compare the activation energies. In this exercise we will learn how to obtain a profile for an ion permeating an engineered peptidic channel. Their cylindric symmetry clearly defines the main pore axis as the reaction coordinates. In this respect, we will effectively project all the forces of the orthogonal degrees of freedom onto the main reaction coordinate, reducing the complexity of the system to a 1D mean interaction potential. Hence the name of Potential of Mean Force.
In equilibrium simulations, the Potential of Mean Force could be extracted by integration of the force the ion feels as it permeates the pore, or by computing the ion number density (probability distribution) along the channel.
As said before, the lack of ion mobility in the time scales available for Molecular Dynamics makes it compulsory to find alternative methods. The common approach is usually to force the ion to sample a given region of the reaction coordinate using an external potential of known characteristics. Umbrella Sampling method restrains the ion at given bins along the channels using a harmonic potential. After removing the force due to the harmonic potential we obtain the underlying Potential of Mean Force. The method needs good sampling of the several bins to achieve a converged equilibrated ensemble, especially critical in the regions where the potential is steep.
Another possibility would be to drive the ion along the pore by means of a guiding harmonic potential: at a given speed, we pull the ions through the pore using a harmonic spring. If done infinitely slowly, the system does not dissipate energy and the work done at a given coordinate equals the Potential of Mean Force.

Molla
But thanks to the non-equilibrium relationships discussed above, we can extract Free Energies out of an ensemble of non-equilibrium trajectories. Here we will use a special application of Crooks' TFT and the fact that our spring force constant will be very high. The method is know as FR method, or Forward-Reverse.



Crooks' TFT and the stiff spring approximation

The stiff spring approximation guarantees that the work distribution obtained is Gaussian. Combining this result with Crooks' TFT, we can see that if the Forward trajectories generate a Gaussian work probability distribution with mean 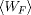and variance sigma, the Reverse probability distribution is also Gaussian with 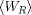mean and the same variance sigma.


Putting all this together, we see that the Potential of Mean Force can be simply computed as the mean of the averaged work in Forward and Reverse direction (the minus sign is due to the definition of the dissipated work). There is no need to compute the overlapping point between the two work distributions, since they are Gaussians with the same variance: the point were they cross is the average of the two mean values.

FR visual

Since generating enough trajectories to estimate a work average in the forward and reverse directions is time consuming, here we will simply work on a set of pre-computed dynamics. For each ion being pulled in either direction, we obtain a file describing the position of the ion and the spring reference position at any time. Given a stiff force constant, that we previously selected (10000 kJ / mol nm^2), it is straightforward to compute the force the system is exerting on the ion as a function of the spring position. Integration of the resulting force along the pore yields the work in a given direction.

Here you will find a multiple entry pdb to visualize a trajectory of an ion being pulled through a channel. Open the file with pymol:

/usr/global/whatif/pymol/pymol pulling_movie.pdb
In Pymol's command line write:

select potassium, name PO1
And in the newly created entry on the main program's window, name (potassium), select "S" and "spheres". You can play the movie using the controls on the lower right side of the main window. Have a look and quit the viewer when satisfied.

Now, remove the movie:

rm -f pulling_movie.pdb


And we start with the actual analysis.

In this folder you will find all the needed files and scripts to follow the exercise. Download it to your account.

First switch to the home folder:

cd

and extract the contents of the folder like we did before:

tar -xvzf ion_FR.tar.gz ; rm -f ion_FR.tar.gz

or, if you downloaded to the default 'Desktop' folder:

tar -xvzf Desktop/ion_FR.tar.gz ; rm -f Desktop/ion_FR.tar.gz

Get in the extracted folder:

cd ion_FR

You will see a couple of folders, one for each channel. If time permits we will compute the Potential of Mean Force for three channels, otherwise we will illustrate the method with just p-ala15.

cd p-ala15_single
As said before, doing multiple simulation runs is very tedious if one has to do everything by hand. We will first compute the work along one of the forward and reverse paths by hand, and afterwards we will use a set of scripts to compute the rest. Firstly, let's extract the work for the forward run,

cd forward_run

Here you will find a pull.pdo file, which contains: the time (ps), a reference position in the channel (we don't need it here), the position of the group being pulled (ion, in our case) and the position of the spring (nm) . Since we know the force applied is harmonic with a force constant of 10000 kJ / mol nm^2, we can easily compute the force,


We will use the following comand to extract the value of the force at each spring position, which moves from one end to the other of the pore,


cat pull.pdo | awk '($1 != "#" && $1 != "#####") {print $3, 10000*($4 - $3)}' > force.txt

With this command for each line of numeric input we print the third column (position) and we compute the force based on the above formula. Finally, the pair of values is put into a file.
Now we will sort the values corresponding to the z axis in ascending order,

sort -n -k 1 force.txt > sorted_forces.txt

Now open the file sorted_forces.txt to perform the integration of the force, which will lead to the work along the path.

xmgrace sorted_forces.txt

Never mind if you get an xmgrace warning. Just close the warning window and proceed. It will not affect the result. As we did before, under "Data", select "Transformations", followed by "Integration", and press "Accept". The integrated curve is now in graph G0.S1. We will write it to a file: select "Data", then "Export" and "ASCII". Select the graph GO.S1 and under "Selection" choose a name, for example forward_work.txt.
Since we would like to average the work in both directions, we will need to make sure that both files have the same number of data points. This can be accomplished by performing a window average: all the data points lying in the interval [z,z+width] will be averaged. Use the following command,

awk -f ../../p-ala15/forward_run/window.awk < forward_work.txt > forward_W_av.txt

Copy the resulting file to the FR_single folder,

cp forward_W_av.txt ../FR_single

Question: If you have a look at the result, with xmgrace, you will see that this result cannot be the correct Potential of Mean force. Why not? Should the potential energy be different at both sides of the channel?

Ok, so now we will repeat the same operations for the reverse path,

cd ../reverse_run

cat pull.pdo | awk '($1 != "#" && $1 != "#####") {print $3, 10000*($4 - $3)}' > force.txt
sort -n -k 1 force.txt > sorted_forces.txt
Integrate the forces the same way as before. Export the result to a file, say reverse_work.txt. Since we have sorted the position in ascending orther, we automatically have switched the sign of the integration. For that reason we can directly compute the average of both Forward and Reverse works to get the Potential of Mean Force. We finally use window average to have a compatible set of data points, like before,

awk -f ../../p-ala15/forward_run/window.awk < reverse_work.txt > reverse_W_av.txt
cp reverse_W_av.txt ../FR_single
cd ../FR_single

Now that we have all the work profiles along the channel, let's use the result we derived for TFT and the stiff spring approximation: average Forward and Reverse work to get the Potential of Mean Force. We will use a tiny script that takes care to average the right values:

./average_work.csh forward_W_av.txt reverse_W_av.txt | grep -v csh > Free_Energy_15.txt

This file contains a reference PMF for this channel. Compare it with the one you just computed and the work performed in the forward and reverse path,

xmgrace ~/Desktop/reference_PMF_ala15.txt Free_Energy_15.txt forward_W_av.txt reverse_W_av.txt

The black curve is the reference Potential of Mean Force and the red curve is the averaged curve we just calculated. The green curve is the forward transition, whereas the blue curve is the reverse transition.

Question: Did the result get better, after averaging? Where is the main barrier for ion permeation through this channel located?

Now that we learned that the approach seems to yield reasonably good results, let's compute a bunch of work profiles in both directions to see how the overall result improves. Since it's a lot of work to do it by hand, we will use scripts that will automate the exact same process you just did,

cd ../../p-ala15
cd forward_run
This script will generate different work profiles for 5 different trajectories in the Forward direction.

./compute_work.csh

Now move all the resulting profiles to the folder where we will average them all,

cp W_fwd_*.txt ../FR_average

To obtain the work in the Reverse direction, let's simply do the same again,

cd ../reverse_run
./compute_work.csh
cp W_rev_*.txt ../FR_average

Now we move to the FR_average folder and perform the averages with the following commands,

cd ../FR_average
./do_averages.csh

Have a loook at the obtained Free Energy (or Potential of Mean Force) profile. Compared it with the previous one using xmgrace:

xmgrace ~/Desktop/reference_PMF_ala15.txt Free_energy.txt



Question: Does the result improve? How does it compare to the reference profile?

D. Optional: further analysis

 Since we already know how to use the Crooks fluctuation theorem to extract potentials of mean force, let's use this method to learn something about ion channels. Following the same procedure, we already computed the work along the trajectory for two channels longer than 15 aminoacids, namely 19 and 25. To compute the Potential of Mean Force, simply move to their FR_results

cd ../../p-ala19/FR_results
./do_averages.csh

Now we align the profile with the previous one:

awk '{print $1-0.3,$2}' Free_energy.txt > t ; mv -f t Free_energy.txt
and look at the two together:

xmgrace Free_energy.txt ../../p-ala15/FR_average/Free_energy.txt
cd ../../p-ala25/FR_results
./do_averages.csh
Again, we align the profile with the previous ones:

awk '{print $1-0.5,$2-5}' Free_energy.txt > t ; mv -f t Free_energy.txt
and look at them together:

xmgrace Free_energy.txt ../../p-ala15/FR_average/Free_energy.txt ../../p-ala19/FR_results/Free_energy.txt

Compare the resulting profiles with the p-ala15.

Question: How does the profile change as we move to longer channels? Would you expect this effect to be linear?

Go back to Contents

Further references: