In the previous lecture we've learned about the importance of long-range electrostatic interactions for an accurate modeling of biomolecular macromolecules in aqueous solution. Today's practical will deal with the computation of these interactions by means of the so-called non-linear Poisson-Boltzmann equation (PBE)
introduced during the last lecture.
In the equation above ![]() is the number density of ions of type i in the bulk solution,
is the number density of ions of type i in the bulk solution,
![]() is the charge on the ion,
is the charge on the ion, ![]() is the electrostatic potential in that region of space,
is the electrostatic potential in that region of space, ![]() is Boltzmann's constant and
is Boltzmann's constant and ![]() is the temperature.
is the temperature.
![]() is the charge density due to the macromolecule under consideration. Note that the dielectric constant epsilon(x,y,z) is a function of the location in R3 (inhomogenous epsilon). The nonlinear PBE given above can be linearized
via a Taylor expansion of the sum at the right hand side (as shown last week).
is the charge density due to the macromolecule under consideration. Note that the dielectric constant epsilon(x,y,z) is a function of the location in R3 (inhomogenous epsilon). The nonlinear PBE given above can be linearized
via a Taylor expansion of the sum at the right hand side (as shown last week).
To obtain solutions of the PBE on a computer, we are going to use APBS (Adaptive Poisson-Boltzmann Solver), a software package for evaluating the electrostatic properties of nanoscale biomolecular systems, which is already installed on the computers you are working with. APBS
solves the Poisson-Boltzmann equation numerically by means of a finite difference/finite element
approach. For more details on this, please see this program web site.
The files needed for this practical can be downloaded here. You will need to unpack
the archive by typing:
wget http://www3.mpibpc.mpg.de/groups/de_groot/compbio2/p11/PBE_prakt.tar.gz tar xzvf PBE_prakt.tar.gz
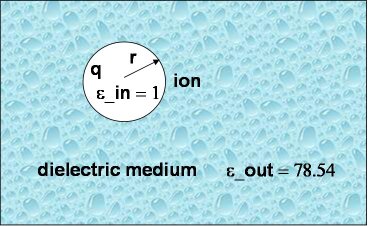 As a first and rather straightforward step we are computing the solvation free energy of a ion with charge q and radius a (or r in the picture to the right) embedded in a dielectric continuum with dielectric constants epsilon_out. The ion itself has a dielectric constant of epsilon_in. In other words, epsilon_in and epsilon_out denotes the internal and external (solution) dielectric constants, respectively. If epsilon_in is chosen to be 1, the result obtained is the free energy change associated with transfering an ion from the gas phase into a solute with dielectric constant epsilon_out.
In our Born solvation model we assume zero ionic strength.
As a first and rather straightforward step we are computing the solvation free energy of a ion with charge q and radius a (or r in the picture to the right) embedded in a dielectric continuum with dielectric constants epsilon_out. The ion itself has a dielectric constant of epsilon_in. In other words, epsilon_in and epsilon_out denotes the internal and external (solution) dielectric constants, respectively. If epsilon_in is chosen to be 1, the result obtained is the free energy change associated with transfering an ion from the gas phase into a solute with dielectric constant epsilon_out.
In our Born solvation model we assume zero ionic strength.
Two things are needed to run a calculation with APBS:
cd born
For our Born solvation model the PQR file only contains one atom with partial charge +1. Type:
more born.pqr
The input file for APBS (apbs.in) is somewhat more extended and looks like this:
# READ IN MOLECULES
read
mol pqr born.pqr # Read molecule 1
end
# CALCULATE POTENTIAL FOR SOLVATED STATE
elec name solvated
mg-manual
dime 65 65 65
nlev 4
grid 0.33 0.33 0.33
gcent mol 1
mol 1
lpbe
bcfl mdh
pdie 1.0 # Solute dielectric
sdie 78.54 # Solvent dielectric
chgm spl2
srfm mol
srad 1.4
swin 0.3
sdens 10.0
temp 298.15
gamma 0.105
calcenergy total
calcforce no
write pot dx pot
end
# CALCULATE POTENTIAL FOR REFERENCE STATE
elec name reference
mg-manual
dime 65 65 65
nlev 4
grid 0.33 0.33 0.33
gcent mol 1
mol 1
lpbe
bcfl mdh
pdie 1.0
sdie 1.0 # Solvent dielectric
chgm spl2
srfm mol
srad 1.4
swin 0.3
sdens 10.0
temp 298.15
gamma 0.105
calcenergy total
calcforce no
end
# COMBINE TO FORM SOLVATION ENERGY
print energy solvated - reference
end
# SO LONG
quit
First, APBS reads the PQR file named born.pqr. Then two PBE calculations with
different solvent dielectric constants, 1 and 78.54 will be
carried out.
Question: why are we using these values?
The two groups are named solvated and reference, and the difference between these two free energies will be printed at the end of the run (Please note: you do not need to know the precise meaning all the other parameter in the APBS input !!!). Let's run APBS by typing
/usr/opt/cbp/apbs-pdb2pqr/apbs/bin/apbs apbs.in
Compare your computed result with the analytical value obtained via
,
where R is the radius of the ion.
Question:
Where does the small error come from?
You can change the radius in the PQR file (last number), repeat the calculation and compare
again the numerical and the analytical result.
We can now also display the electrostatic potential by typing
vmd -e pot_field.vmd
Have a look at the structure of helical gA dimer by typing (first change into the correct folder)
cd ../gA vmd -e gA.vmd
and rotating the polypeptide.
Also have a look at the SYSTEM.pqr file.
Question:
What is so far the (only) major difference compared to the previous Born ion example?
At this point we need to specify the internal (i.e. inside the protein) dielectric constant for our calculation
(remember: in the Born solvation case the internal dielectric constant was set to 1).
With the dielectric constant being a macroscopic observable, but the biomolecular macromolecule
being a nano-sized molecular entity, it is often not clear what value
to choose, and one should consider the internal dielectric constant as an
adjustable parameter within the PBE framework. It usually ranges from 2 to 20,
depending on the molecular details of the macromolecule under consideration.
Question:
What determines the lower bound of the range?
We can now easily perform the PBE calculation inside VMD. VMD - Visual Molecular Dynamics - is a molecular visualization program for displaying, animating, and analyzing large biomolecular systems using 3-D graphics and built-in scripting.
Change the values of the isocontours and look what is happening to the molecular representations. The isurface value correspond to value of the electrostatic
potential as computed by the PB solver.
If VMD is not functioning properly you can download the snapshots of the electrostatic potential isosurfaces.
One can also map the electrostatic potential onto a generated molecular surface. For example one can compute the so-called solvent-accessible surface by rolling a contact sphere with a given radius over the macromolecule and then grouping (triangulating) all sphere center points into one surface.
Now you can zoom into the channel region. The striking feature is that the
channel area as well as the entrance area show the same coloring, which means
the sign of the potential is the same.
Question:
What sign of
the potential whould you expect for a cation selective channel (i.e. a channel
that permeates positively charged ions)?
We can check on the sign of the potential by inspecting the coloring scheme used in the representation.
To do so we go to "Graphics -> Color" menu in the main window, then the Color Scale tab. If you prefer the opposite red-blue scale, change the dropdown to BWR (or any other scale).

cd ../gA_ion
ATOM 547 HA2 ETA 17 2.016 -10.455 -4.104 0.090 1.320 ATOM 548 CB ETA 17 2.566 -12.311 -5.091 0.050 2.175 ATOM 549 HB1 ETA 17 2.983 -13.305 -4.818 0.090 1.320 ATOM 550 HB2 ETA 17 1.624 -12.457 -5.663 0.090 1.320 ATOM 551 OG ETA 17 3.493 -11.626 -5.922 -0.660 1.770 ATOM 552 HG1 ETA 17 3.762 -12.236 -6.614 0.430 0.224 ATOM 553 Na ION 3 -2.675 16.000 -1.764 1.000 1.908 END
We can also have a look at the sequence of differing ion positions inside gA by typing
vmd -e snapshots.vmd
As in the Born solvation example, we also need to compute a reference state that only
contains the cation embedded in pure water ( those coordinates can be found in the ion.pqr.* files: have a look at one of them).
If we substract the two computed free energies we get the difference in free energy
between the cation being solvated by pure water and the cation being solvated at a fixed position by gA, which is hydrated by water (Note that we are only interested in the free energy difference, so no complete thermodynamic cycle needs to be computed!). The working directory contains a script that will
perform the 9 independend pairs of PBE calculations and write the total free energy into a file
named "total_energy". The APBS parameters are given in apbs.in
Question:
What solute dielectric constant
is initially used?
You can now start the script by typing
./PBE_loop
For each snapshot shown the script will run a PBE calculation and extract the solvation free energy difference.
After the calculation is finished, you can plot the free energy profile using e.g. "gnuplot"
gnuplot plot "total_energy" w lp plot "total_energy" u :1 smooth csplines w lp
Question:
Why should the profile be symmetric? Why is it not the case?
You can now change the solute dielectric constant in the "apbs.in" file, repeat the previous
computation cycle and try to reproduce the plot shown below, using different
values of epsilon.
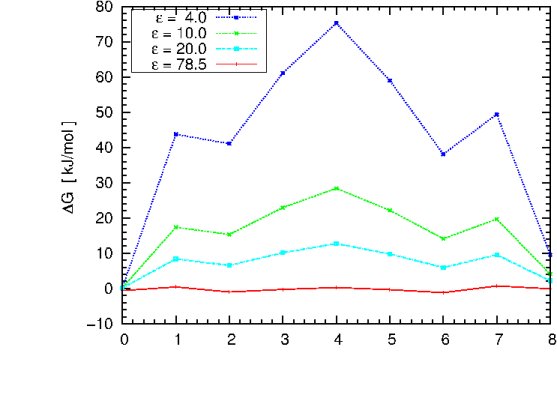
The graph illustrates the dependence of the free energy profile
as a function of the protein dielectric constant. The free energy barrier for Na+ migration
through gA is estimated to be ~ 50 kJ/mol.
Question:
Which dielectric constant will give a result close to
experiment? Which dielectric constant would you choose if there would be no experimental value
to compare with?
Question:
What can we learn from this plot? Does it have the correct asymptotic behaviour as epsilon_in approaches 78.54?
Question:
An alternative would be to estimate the free energy profile from MD
simulations of the gramicidin channel embedded in a lipid bilayer membrane
surrounded by water. In such MD simulations, the dielectric constant is
usually set to 1. How do you expect that choice to affect the result?
Question:
Which other main difference can you think of, relative to MD simulations?
Further references