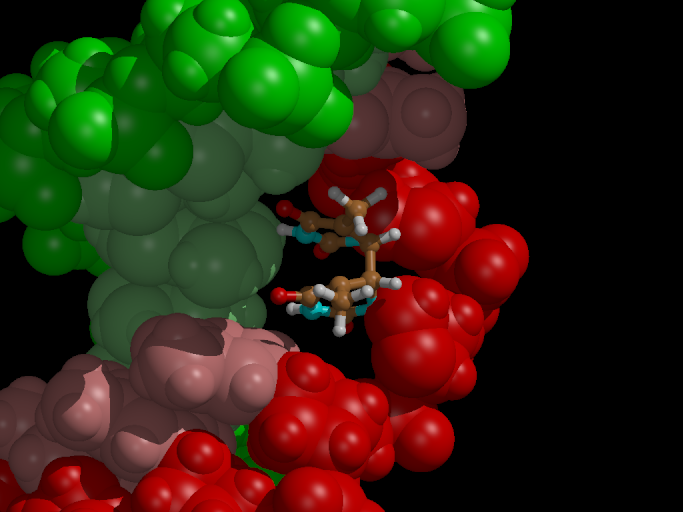
 Now we want to study the effect of an electron uptake on the dimerized
thymine, as conducted in the presence of the enzyme Photolyase (see
introduction). Will the (unhealthy) bond break?
Now we want to study the effect of an electron uptake on the dimerized
thymine, as conducted in the presence of the enzyme Photolyase (see
introduction). Will the (unhealthy) bond break?
In the previous lectures, you learned about quantum chemical methods that allow one to compute the electronic structure of molecules. In this practical, we will use these methods to study a chemical reactions of a DNA molecule. To be more precise, we study the dimerization of thymine within a DNA double strand.
Classical MD simulations, based on Newton's equations of motion and classical force fields, are quite efficient and allow simulations on time scales up to microseconds or even longer. A number of such simulations were conducted in the practicals of the last semester. However, classical force field cannot describe the formation or breaking of chemical bonds Thus, if we wish to study chemical reactions, we must describe the molecular system using quantum mechanical methods. Unfortunately, these are orders of magnitude more expensive and scale unfavorably with the number of atoms. As a consequence, we cannot describe a complete biomolecule (protein, DNA, ...) quantum-mechanically.
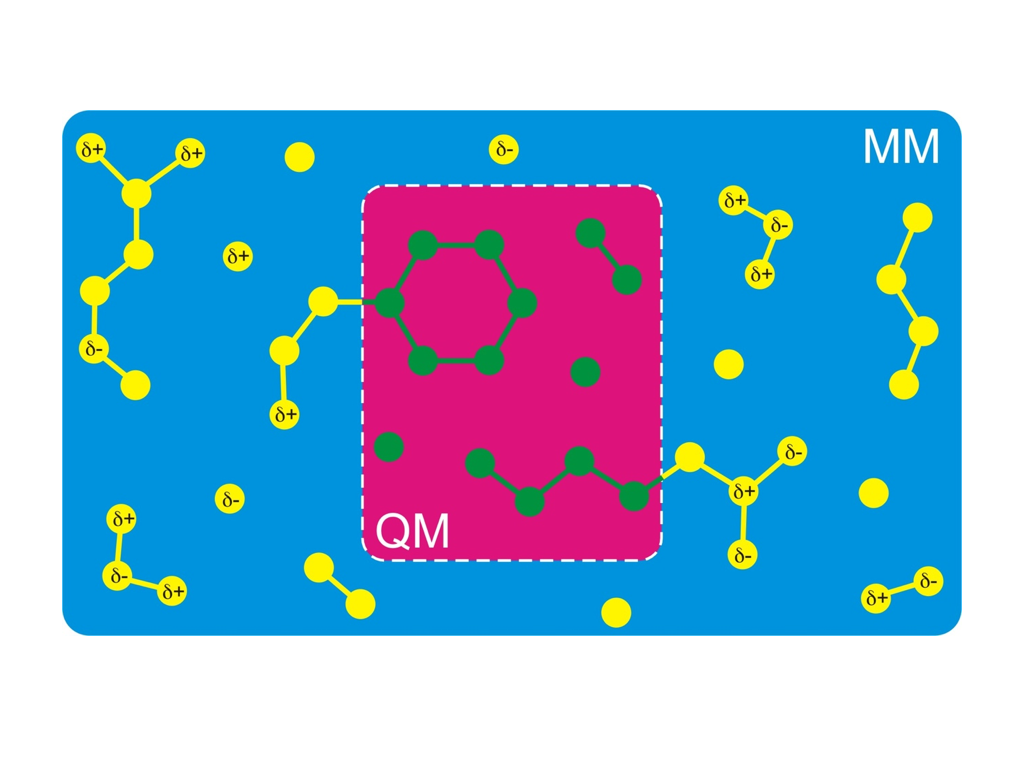
A simulation technique that nevertheless allows you to simulate the chemistry of biomolecules is called hybrid QM/MM (quantum mechanics/molecular mechanics). The idea is to treat only that part of the molecule quantum mechanically, where the chemical reaction takes place (red background in the figure on the right-hand side). The rest is treated using a normal classical Newtonian dynamics and classical force field (blue background in the figure). Notably, the Nobel Price for Chemistry was awarded in 2013 to Martin Karplus, Michael Levitt, and Arieh Warshel for the development of the QM/MM method.
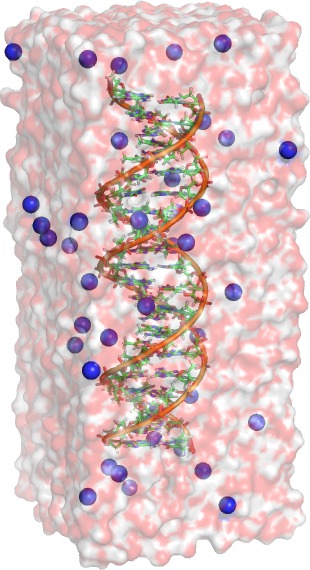
As mentioned above, we here study the dimerization of the nucleotide thymine within one strand of a DNA double helix. Intra-strand thymine dimerization (see figure above) is recognized as the most common process leading to DNA damage under ultraviolet (UV) irradiation. The formation of thymine dimers has potentially important physiological consequences. This mutagenic photoproduct can disrupt the function of DNA and thereby trigger complex biological responses, including apoptosis (triggered cell death), immune suppression, and carcinogenesis (development of cancer). To survive the exposure to UV radiation, organisms have evolved complex mechanisms to repair damaged DNA. The initial step is usually the detection of a damage spot, a thymine dimer for instance. Subsequently, the dimer is either repaired, or completely removed.
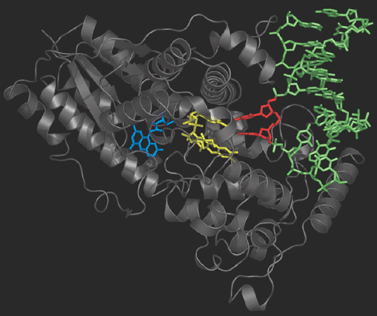
Photolyase is an enzyme that detects the dimer site by binding to it and then catalyses the splitting of the dimer into the original pyrimidine bases (figure on the right). Photolyase contains a reduced flavin co-enzyme co-factor that upon absorption of UV light donates an electron to the bound Thyime dimer. The excess electron destabilizes the dimer, and facilitates the slitting of the cyclobutane ring. After the original thymine bases are restored, the electron flows back onto the flavin and Photolyase is ready to repair the next lesion.
Thymine dimers can also be restored without the help of Photolyase. In this so-called self-repair process, the dimer splits upon spontaneous uptake of an electron. Depending on the base sequence, such electrons are readily available. In this tutorial we will examine the self repair process by means of QM/MM simulations.
In the following, we set up a simulation system of a DNA double helix
solvated in water. A PDB structure of an helix and the required force
field files can be found here.
Please note that the commands in the gray boxes can be easily transferred to the
command prompt with copy-and-paste (select text by dragging the mouse over it
with the left mouse button pressed, and paste by pressing the middle mouse
button).
Unpack the gzipped tar ball with
tar xvzf setup-helix.tar.gz
The simulations will be carried out with the GROMACS simulation package. On the GROMACS homepage you can find both the software and documentation (online reference and paper manual). To run a simulation, three input files are usually required:
Any GROMACS command is executed via a single Linux executable, named gmx. As shown below, a specific GROMACS command gromacscommand is called via a call such as:
gmx gromacscommand options...
 First, we generate a topology with the Gromacs command
pdb2gmx. The file helix.pdb contains two special thymine
types with residue names DTa and DTb, respectively. pdb2gmx will read
the residue topology database amber99.ff/dna.rtp, in which two special
chemical bonds between DTa and DTb are defined. These two bonds make
the dimer. Run:
First, we generate a topology with the Gromacs command
pdb2gmx. The file helix.pdb contains two special thymine
types with residue names DTa and DTb, respectively. pdb2gmx will read
the residue topology database amber99.ff/dna.rtp, in which two special
chemical bonds between DTa and DTb are defined. These two bonds make
the dimer. Run:
gmx pdb2gmx -ignh -f helix.pdb -o conf.pdb
Hint: ls -lrt prints the files in the current directory, with the most recent files at the bottom. So you can easily see which files were written by the last command.
Next, we place the structure written by pdb2gmx into a simulation box (using the editconf command), and we add water to the simulation box:
gmx editconf -c -d 1.0 -f conf.pdb -o boxed.pdb
gmx solvate -cs spc216.gro -cp boxed.pdb -p topol -o solved.pdb
gmx grompp -f neutralize.mdp -c solved.pdb
gmx genion -np 38 -pname NA -o neutral.pdb -p
Take a look for instance in rasmol (type rasmol neutral.pdb) to have a look at the system. To see the ions, use the command select Na and choose in the menu Display->Spacefill. In addition, switch on the box by unitcell on. You can also use PyMOL or VMD if you prefer.
Now, the structure is in a state of high-energy because of two reasons. (a) potential overlap between added water molecules and DNA; (b) because the chemical bonds that connect the thymine monomers are not relaxed. Therefore, we carry our an energy minimization using the steepest descent algorithm.
gmx grompp -f steep.mdp -c neutral.pdb gmx mdrun -v -c neutral_mini.pdb
gmx grompp -f equil.mdp -c neutral_mini.pdb gmx mdrun -v -c equil.pdb
egrep -v ' NA | SOL' neutral_mini.pdb > neutral_mini_dna.pdb
vmd neutral_mini_dna.pdb traj.xtc
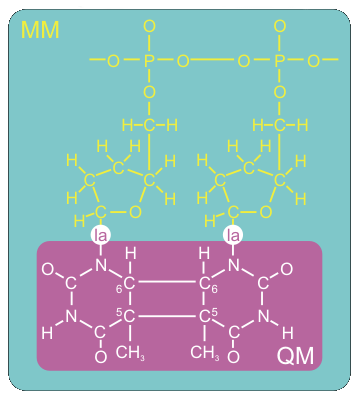
We want to set up the system for a QM/MM simulation with Gromacs. The dimerized thymine bases will be described at the semi-empirical AM1 level of theory, while the remainder of the system is modeled with the Amber99 forcefield. Figure 3 shows how we split up our system in a QM and MM part.
The QM/MM division splits the systems along a chemical bond. Therefore, we need to cap the QM subsystem with a so-called link atom (la in the figure). This link atom is present as a hydrogen atom in the QM calculation step. It is not physically present in the MM subsystem, but the forces on it, that are computed in the QM step, are distributed over the two atoms of the bond. The bondlength itself is constrained during the computations.
To make use of the QM/MM functionality in Gromacs, we have to
tar xvzf qmmm-system.tar.gz
Have a look into the structure file qmmm1.gro and into the topology qmmm.top. You will find the link atoms with atom name LA. Note that they are defined at so-called dummies (or "virtual sites") near the end of the topology. That means that they do not take part in the Newtonian dynamics - instead, their positions are constructed at each step based on the positions of nearby atoms.
Open the MD parameter file qmmm1.mdp, where the details of the QM calculation are defined. Add the keyword AM1 for the option QMmethod, and the basis STO-3G for option QMbasis. For now, the dimer is neutral (set QMcharge to zero). What is the spin multiplicity (QMmult) if we have fully occupied orbitals?
Let's start your first QM/MM simulation of 1ps. For this part, we need a special mdrun binary that has been linked with the MOPAC library. MOPAC (Molecular Orbital PACkage) is a semiempirical quantum chemistry program. That mdrun and a suitable grompp been added to the tar ball. Make the two binaries executable (chmod +x) and use
./grompp -c qmmm1.gro -f qmmm1.mdp -n qmmm -p qmmm -o qmmm1.tpr ./mdrun -v -stepout 1 -deffnm qmmm1 -c qmmm1out.pdb
export LD_LIBRARY_PATH=$(pwd)
egrep -v ' Na | SOL' qmmm1out.pdb > qmmm1out_dna.pdb
vmd qmmm1out_dna.pdb qmmm1.xtc
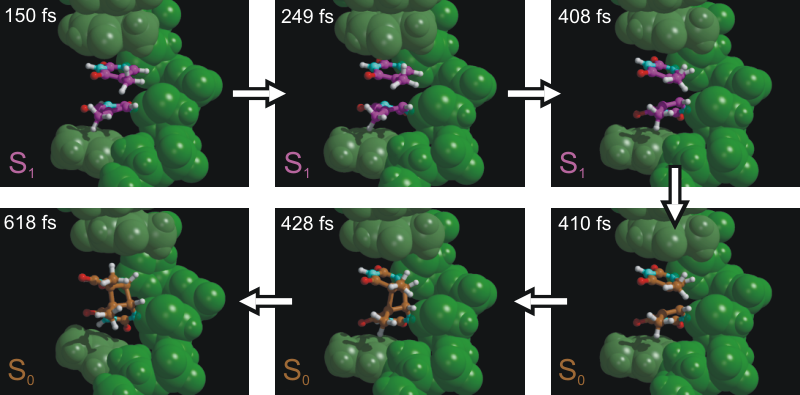
 Now we want to study the effect of an electron uptake on the dimerized
thymine, as conducted in the presence of the enzyme Photolyase (see
introduction). Will the (unhealthy) bond break?
Now we want to study the effect of an electron uptake on the dimerized
thymine, as conducted in the presence of the enzyme Photolyase (see
introduction). Will the (unhealthy) bond break?
./grompp -f qmmm2.mdp -c qmmm1out.pdb -n qmmm -p qmmm -o qmmm2.tpr ./mdrun -v -stepout 1 -deffnm qmmm2 -c qmmm2out.gro
vmd qmmm1out_dna.pdb qmmm2.xtc
Question: Is the dimer stable, or does a bond break? Which bond is breaking? Can you speculate why this and not the other bond breaks?
A final note: the first bond broke in less than a picosecond, suggesting that this first rupture is essentially barrierless. If we would simulate much longer, the second barrier would eventually break as well - on a much longer time scale. In order to observe the rupture, alternative simulations techniques are required such as the calculation of free-energy profiles or conformational flooding. These are, however, beyond the scope of this practical.
Hope you enjoyed it. In case of questions or suggestions, please do not hesitate to contact Bert de Groot: bgroot@gwdg.de