

Next: A Markov Model
Up: Conformational Dynamics
Previous: Theory of Conformational
We now try to describe the dynamics of our protein model in the vicinity
of the energy minimum `D' (cf. Fig.  ) as a Brownian motion.
As a conformational coordinate, we chose the distance
) as a Brownian motion.
As a conformational coordinate, we chose the distance  ,
which allows to separate substate `B' from substate `D'
(cf. Fig.
,
which allows to separate substate `B' from substate `D'
(cf. Fig.  ). Since the dynamics within substate `D'
determines the transition rate
from `D' to `B',
comparison of this particular rate determined from the Langevin
model with the corresponding rate observed in the simulation will provide
a check whether that model is applicable.
). Since the dynamics within substate `D'
determines the transition rate
from `D' to `B',
comparison of this particular rate determined from the Langevin
model with the corresponding rate observed in the simulation will provide
a check whether that model is applicable.
The time evolution of the stochastic model
is described by the Langevin equation:
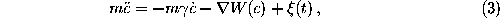
where m denotes the effective
mass[69] of a Brownian particle, the motion of
which is governed by a heat bath a potential of mean force, 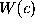 .
The influence of the heat bath is described by the friction coefficient
.
The influence of the heat bath is described by the friction coefficient
 and a fluctuating force
and a fluctuating force
 .
The dots represent time derivatives.
We assume, that
.
The dots represent time derivatives.
We assume, that  can be modelled by Gaussian (white) noise, and then we check, whether
this assumption, which implies a neglect of memory effects, is correct.
can be modelled by Gaussian (white) noise, and then we check, whether
this assumption, which implies a neglect of memory effects, is correct.
Figure  (left) shows the
potential of mean force,
(left) shows the
potential of mean force,  , which
has been computed according to (
, which
has been computed according to ( ) and (
) and ( ),
respectively,
where only those conformations, which belong to state D or B, have been
used for the calculation of
),
respectively,
where only those conformations, which belong to state D or B, have been
used for the calculation of 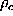 according to (
according to ( ).
The considerable length of the trajectory allowed a quite accurate
determination of
).
The considerable length of the trajectory allowed a quite accurate
determination of  . As a check, we computed
. As a check, we computed
 using only
half of the trajectory. Compared to the full statistics,
no significant deviations were observed (data not shown).
using only
half of the trajectory. Compared to the full statistics,
no significant deviations were observed (data not shown).
In Fig.  the transition under consideration,
the transition under consideration, 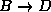 ,
corresponds to a transition from the deep minimum across
the energy barrier to the left. To calculate
its rate from the Langevin model, the parameters m and
,
corresponds to a transition from the deep minimum across
the energy barrier to the left. To calculate
its rate from the Langevin model, the parameters m and
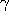 have to be specified; the amplitude of
have to be specified; the amplitude of 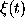 then follows
from the dissipation fluctuation theorem.
then follows
from the dissipation fluctuation theorem.
As indicated by harmonic fits (dashed lines) in Fig.  (left),
at the energy minimum and at the barrier top, the shown energy landscape
can be described by a harmonic double well.
Diffusive motion in such a double well potential can be
described analytically and, therefore, enables a
simple determination of the friction coefficient
(left),
at the energy minimum and at the barrier top, the shown energy landscape
can be described by a harmonic double well.
Diffusive motion in such a double well potential can be
described analytically and, therefore, enables a
simple determination of the friction coefficient  as well
as of the effective mass m, which enter into
(
as well
as of the effective mass m, which enter into
( ) as adjustable parameters, from our simulations.
For that purpose, we make
use of the velocity autocorrelation function,
) as adjustable parameters, from our simulations.
For that purpose, we make
use of the velocity autocorrelation function,
 , computed from an average
using a selected 1ns-trajectory, which did not leave state 'D'.
In our harmonic approximation we assume
, computed from an average
using a selected 1ns-trajectory, which did not leave state 'D'.
In our harmonic approximation we assume
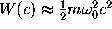 .
.
 can then be derived analytically
and
can then be derived analytically
and 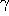 can be determined by comparison with the simulation.
We used the velocity autocorrelation
instead of a displacement correlation, because it relaxes more rapidly,
its relaxation depends sensitively on the friction coefficient, and
it is rather insensitive to the characteristics of the mean force
potential[57].
can be determined by comparison with the simulation.
We used the velocity autocorrelation
instead of a displacement correlation, because it relaxes more rapidly,
its relaxation depends sensitively on the friction coefficient, and
it is rather insensitive to the characteristics of the mean force
potential[57].
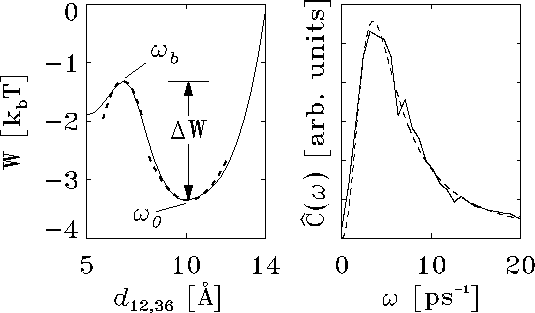
Figure: Left: potential of mean force  for the conformational
coordinate c in
units of
for the conformational
coordinate c in
units of 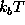 (solid line); harmonic fits as described in the text
are shown as dashed lines; right: low-frequency part of the
spectrum
(solid line); harmonic fits as described in the text
are shown as dashed lines; right: low-frequency part of the
spectrum 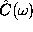 of the autocorrelation function
of the autocorrelation function
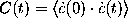 derived from a
1-ns-trajectory (bold line); fit of an expression derived from
a harmonic oscillator model (dashed line).
derived from a
1-ns-trajectory (bold line); fit of an expression derived from
a harmonic oscillator model (dashed line).
Figure  (right) shows
the low-frequency part of the spectrum of
(right) shows
the low-frequency part of the spectrum of  (solid line).
In the diffusive harmonic oscillator model
the spectral density of the velocity
autocorrelation function is given
by [69]
(solid line).
In the diffusive harmonic oscillator model
the spectral density of the velocity
autocorrelation function is given
by [69]
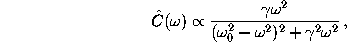
provided that 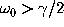 , which is assumed to
hold for the present application.
A fit (dashed line) of this expression to the low-frequency part
of the observed velocity autocorrelation
spectrum yields
, which is assumed to
hold for the present application.
A fit (dashed line) of this expression to the low-frequency part
of the observed velocity autocorrelation
spectrum yields  and
and
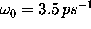 . In the harmonic oscillator model, this
corresponds to an effective mass of
. In the harmonic oscillator model, this
corresponds to an effective mass of 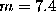 atomic units.
The excellent quality of the fit demonstrates the applicability
of the harmonic oscillator model. Moreover, the obtained values for
atomic units.
The excellent quality of the fit demonstrates the applicability
of the harmonic oscillator model. Moreover, the obtained values for
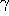 and
and
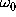 , respectively, justify the assumption of
moderate friction
(
, respectively, justify the assumption of
moderate friction
( ).
).
An upper limit  for the transition rate in the case of
moderate friction can be obtained using Kramers' theory[70],
for the transition rate in the case of
moderate friction can be obtained using Kramers' theory[70],
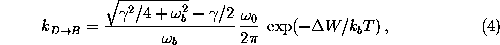
where 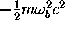 is a
harmonic fit to the potential at the
barrier top b (cf. Fig.
is a
harmonic fit to the potential at the
barrier top b (cf. Fig.  (left)) and
(left)) and
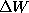 is the
barrier height. With
is the
barrier height. With 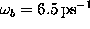 one obtains
one obtains
 . However, this prediction
largely overestimates the rate obtained
from the MD-simulation, which is lower by a factor of nearly 25, namely
. However, this prediction
largely overestimates the rate obtained
from the MD-simulation, which is lower by a factor of nearly 25, namely
 !
!
Obviously, the Langevin model
could not reproduce the observed conformational transition rates.
This failure must be attributed to the only unjustified assumption in that
model, namely that of memory-free, Gaussian noise as a description of the
influence of all degrees of freedom within the system on the dynamics of the
conformational coordinate c. Thus one is forced to the conclusion,
that memory effects, caused by correlations between many degrees of freedom,
strongly influence the short time scale dynamics within conformational states
at a picosecond time scale. One consequence of these memory effects is
a 25-fold reduction of the particular transition rate under consideration.
A closer inspection of the MD-trajectories showed indeed a frequent
crossing of the barrier top in Fig.  (left), as predicted by
(
(left), as predicted by
( ), but, in most cases,
without a consecutive transition, i.e., the system `remembered', where
it came from. Presumably, a better estimate for the transition rate
could be obtained by applying the method of reactive
flux[22] (a review can be found in Ref. Haenggi90).
However, this method requires the
preparation of an ensemble near the barrier top. The question, whether
this is possible without relying on extended conformational sampling,
must be left open within the present paper.
), but, in most cases,
without a consecutive transition, i.e., the system `remembered', where
it came from. Presumably, a better estimate for the transition rate
could be obtained by applying the method of reactive
flux[22] (a review can be found in Ref. Haenggi90).
However, this method requires the
preparation of an ensemble near the barrier top. The question, whether
this is possible without relying on extended conformational sampling,
must be left open within the present paper.

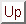

Next: A Markov Model
Up: Conformational Dynamics
Previous: Theory of Conformational
Helmut Grubmueller
Mon Nov 6 16:25:56 MET 1995
 ) as a Brownian motion.
As a conformational coordinate, we chose the distance
) as a Brownian motion.
As a conformational coordinate, we chose the distance  ,
which allows to separate substate `B' from substate `D'
(cf. Fig.
,
which allows to separate substate `B' from substate `D'
(cf. Fig.  ). Since the dynamics within substate `D'
determines the transition rate
from `D' to `B',
comparison of this particular rate determined from the Langevin
model with the corresponding rate observed in the simulation will provide
a check whether that model is applicable.
). Since the dynamics within substate `D'
determines the transition rate
from `D' to `B',
comparison of this particular rate determined from the Langevin
model with the corresponding rate observed in the simulation will provide
a check whether that model is applicable.


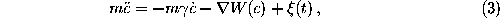
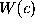 .
The influence of the heat bath is described by the friction coefficient
.
The influence of the heat bath is described by the friction coefficient
 and a fluctuating force
and a fluctuating force
 .
The dots represent time derivatives.
We assume, that
.
The dots represent time derivatives.
We assume, that  can be modelled by Gaussian (white) noise, and then we check, whether
this assumption, which implies a neglect of memory effects, is correct.
can be modelled by Gaussian (white) noise, and then we check, whether
this assumption, which implies a neglect of memory effects, is correct.
 , which
has been computed according to (
, which
has been computed according to (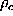 according to (
according to ( . As a check, we computed
. As a check, we computed
 using only
half of the trajectory. Compared to the full statistics,
no significant deviations were observed (data not shown).
using only
half of the trajectory. Compared to the full statistics,
no significant deviations were observed (data not shown).
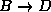 ,
corresponds to a transition from the deep minimum across
the energy barrier to the left. To calculate
its rate from the Langevin model, the parameters m and
,
corresponds to a transition from the deep minimum across
the energy barrier to the left. To calculate
its rate from the Langevin model, the parameters m and
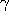 have to be specified; the amplitude of
have to be specified; the amplitude of 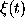 then follows
from the dissipation fluctuation theorem.
then follows
from the dissipation fluctuation theorem.
 as well
as of the effective mass m, which enter into
(
as well
as of the effective mass m, which enter into
( , computed from an average
using a selected 1ns-trajectory, which did not leave state 'D'.
In our harmonic approximation we assume
, computed from an average
using a selected 1ns-trajectory, which did not leave state 'D'.
In our harmonic approximation we assume
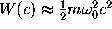 .
.
 can then be derived analytically
and
can then be derived analytically
and 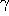 can be determined by comparison with the simulation.
We used the velocity autocorrelation
instead of a displacement correlation, because it relaxes more rapidly,
its relaxation depends sensitively on the friction coefficient, and
it is rather insensitive to the characteristics of the mean force
potential[
can be determined by comparison with the simulation.
We used the velocity autocorrelation
instead of a displacement correlation, because it relaxes more rapidly,
its relaxation depends sensitively on the friction coefficient, and
it is rather insensitive to the characteristics of the mean force
potential[
 for the conformational
coordinate c in
units of
for the conformational
coordinate c in
units of 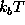 (solid line); harmonic fits as described in the text
are shown as dashed lines; right: low-frequency part of the
spectrum
(solid line); harmonic fits as described in the text
are shown as dashed lines; right: low-frequency part of the
spectrum 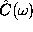 of the autocorrelation function
of the autocorrelation function
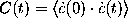 derived from a
1-ns-trajectory (bold line); fit of an expression derived from
a harmonic oscillator model (dashed line).
derived from a
1-ns-trajectory (bold line); fit of an expression derived from
a harmonic oscillator model (dashed line). (solid line).
In the diffusive harmonic oscillator model
the spectral density of the velocity
autocorrelation function is given
by [
(solid line).
In the diffusive harmonic oscillator model
the spectral density of the velocity
autocorrelation function is given
by [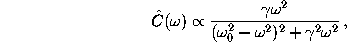
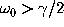 , which is assumed to
hold for the present application.
A fit (dashed line) of this expression to the low-frequency part
of the observed velocity autocorrelation
spectrum yields
, which is assumed to
hold for the present application.
A fit (dashed line) of this expression to the low-frequency part
of the observed velocity autocorrelation
spectrum yields  and
and
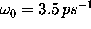 . In the harmonic oscillator model, this
corresponds to an effective mass of
. In the harmonic oscillator model, this
corresponds to an effective mass of 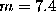 atomic units.
The excellent quality of the fit demonstrates the applicability
of the harmonic oscillator model. Moreover, the obtained values for
atomic units.
The excellent quality of the fit demonstrates the applicability
of the harmonic oscillator model. Moreover, the obtained values for
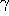 and
and
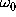 , respectively, justify the assumption of
moderate friction
(
, respectively, justify the assumption of
moderate friction
( ).
).
 for the transition rate in the case of
moderate friction can be obtained using Kramers' theory[
for the transition rate in the case of
moderate friction can be obtained using Kramers' theory[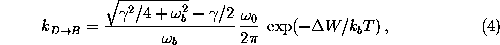
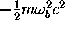 is a
harmonic fit to the potential at the
barrier top b (cf. Fig.
is a
harmonic fit to the potential at the
barrier top b (cf. Fig. 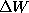 is the
barrier height. With
is the
barrier height. With 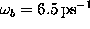 one obtains
one obtains
 . However, this prediction
largely overestimates the rate obtained
from the MD-simulation, which is lower by a factor of nearly 25, namely
. However, this prediction
largely overestimates the rate obtained
from the MD-simulation, which is lower by a factor of nearly 25, namely
 !
!