
Next: About this document
Up: No Title
Previous: No Title
References
- 1
-
E.-L. Florin, V. T. Moy, H. E. Gaub, Science 264, 415 (1994);
V. T. Moy, E.-L. Florin, H. E. Gaub, Science 266, 257 (1995).
- 2
-
The figure was prepared with the use of MOLSCRIPT, P. J. Kraulis, J.\
Appl. Crystallogr. 24, 946 (1991).
- 3
-
G. U. Lee, D. A. Kidwell, R. J. Colton, Langmuir 10, 354 (1994).
- 4
-
N. M. Green, Adv. Protein Chem. 29, 85 (1975); O. Livnah,
E. A. Bayer, M. Wilchek, J. L. Sussman, Proc. Natl. Acad. Sci. USA
90, 5076 (1993).
- 5
-
S. Miyamoto and P. A. Kollman, Proteins 16, 226 (1993).
- 6
-
Reviewed in R. Elber, in New developments in theoretical studies of
proteins, R. Elber, Ed. (World Scientific, Tai Seng, Singapore, in press).
- 7
-
J. A. McCammon, B. R. Gelin, M. Karplus, Nature (London) 267,
585 (1977); W. F. van Gunsteren and H. J. C. Berendsen, Mol.\
Phys. 34, 1311 (1977).
- 8
-
For algorithmic advances, see C. Niedermeier and P. Tavan, J. Chem.\
Phys. 101, 734 (1994); M. Eichinger, H. Grubmüller, H. Heller, P.
Tavan (in preparation); and H. Grubmüller, Phys. Rev. E
52, 2893 (1995) and references therein. For parallel computing,
see [19] and H. Heller, H. Grubmüller, K. Schulten,
Mol. Simul. 5, 133 (1990).
- 9
-
Alternatively, one may compute the free energy profile along the unbinding
reaction path from the MD simulation and derive the rupture force from that
profile. However, because free energies pertain to systems in equilibrium,
this suggested equilibrium approach rests on the questionable assumption that
the rupture is a quasistationary process. Furthermore, it requires
computations of free energies that notoriously exhibit slow convergence.
Thus, in the case at hand our non-equilibrium approach appears to be more
appropriate and is computationally less expensive.
- 10
-
P. C. Weber, D. H. Ohlendorf, J. J. Wendoloski, F. R. Salemme, Science
243, 85 (1989). The x-ray structure contains only residues 13 through
133 of the total of 159 residues. However, this cleavage does not
considerably affect the binding affinity. The structure suggests that the
interaction between the loop containing TRP 120 of the neighboring
streptavidin monomer and the biotin in the binding pocket is considerably
weaker than that for avidin [4].
- 11
-
The simulations were performed with the program EGO [19], which
uses the CHARMM force field [20]. New multi-scale
approximations [8] enabled us to consider the full
Coulomb interaction (with a dielectric constant equal to 1) --- that is, no
cut-off [20] was applied. For biotin, the partial charges were
taken from [5], and the force constants from [21]. All
simulations were carried out with an integration step size of
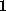 fs. The
lengths of chemical bonds involving hydrogen atoms were fixed [7],
non-polar hydrogen atoms were described through compound
atoms [20], and no explicit term for the hydrogen bond energy was
included. To quantify the strength of hydrogen bonds we used a combination of
energetic (mainly electrostatics) and steric criteria, as suggested
in [22]. The protein--ligand-complex was placed within a
sphere of TIP3 [23] water molecules with a diameter of
fs. The
lengths of chemical bonds involving hydrogen atoms were fixed [7],
non-polar hydrogen atoms were described through compound
atoms [20], and no explicit term for the hydrogen bond energy was
included. To quantify the strength of hydrogen bonds we used a combination of
energetic (mainly electrostatics) and steric criteria, as suggested
in [22]. The protein--ligand-complex was placed within a
sphere of TIP3 [23] water molecules with a diameter of 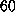 Å\
(
Å\
(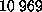 total atoms). All surface water molecules were subjected to
deformable boundary forces [24] [approximated by a quartic
polynomial [20]] and coupled to a heat bath of
total atoms). All surface water molecules were subjected to
deformable boundary forces [24] [approximated by a quartic
polynomial [20]] and coupled to a heat bath of
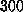 K [19] with a coupling coefficient (
K [19] with a coupling coefficient (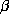 ) of
) of
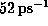 . Additionally, all atoms were weakly coupled to the heat
bath (
. Additionally, all atoms were weakly coupled to the heat
bath (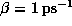 ). After minimization, the system was
equilibrated for
). After minimization, the system was
equilibrated for 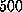 ps because it exhibited relaxations for more than
ps because it exhibited relaxations for more than
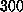 ps. After relaxation the protein backbone atoms showed a root mean
square deviation from the x-ray structure of
ps. After relaxation the protein backbone atoms showed a root mean
square deviation from the x-ray structure of 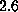 Å. Closer inspection
revealed that a large fraction of the observed deviation arose from two loops
(residues 65 to 70 and 112 to 122) at the tetramer interface, both of which
are flexible in our monomer model but fixed by intermolecular interactions in
the tetramer. The geometry of the binding pocket in our model does not
deviate significantly from that of the x-ray structure (root mean square
deviation
Å. Closer inspection
revealed that a large fraction of the observed deviation arose from two loops
(residues 65 to 70 and 112 to 122) at the tetramer interface, both of which
are flexible in our monomer model but fixed by intermolecular interactions in
the tetramer. The geometry of the binding pocket in our model does not
deviate significantly from that of the x-ray structure (root mean square
deviation 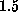 Å). Structures randomly extracted from a subsequent MD run
of
Å). Structures randomly extracted from a subsequent MD run
of 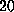 ps in duration were used for the simulations described in the text.
ps in duration were used for the simulations described in the text.
- 12
-
This choice allows thermal fluctuations for
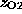 of roughly
of roughly 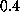 Å
, a value commonly observed for unperturbed atomic fluctuations in proteins.
Therefore, the thermal motion of the pulled atom is essentially unaffected by
the spring potential.
Å
, a value commonly observed for unperturbed atomic fluctuations in proteins.
Therefore, the thermal motion of the pulled atom is essentially unaffected by
the spring potential.
- 13
-
We note that thermal fluctuations entail a logarithmic dependency of the
rupture force on the pulling velocity [3]; however, for
the large velocities studied in our simulations a linear dependency due to
friction dominates. This friction heats the binding region by at most
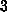 K
in the case of our slowest simulation. That heat is then effectively
transferred to the heat bath; see [11].
K
in the case of our slowest simulation. That heat is then effectively
transferred to the heat bath; see [11].
- 14
-
The computed force profiles exhibit fast fluctuations caused by (artificial)
resonance of our spring. Accordingly, by simply taking the maximum force from
these unprocessed profiles one overestimates the rupture force. Therefore,
before computing rupture forces, we removed the fast fluctuations by
smoothing the force profiles with a Gaussian distribution of
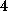 ps width;
that width has been estimated from the decay of the position autocorrelation
function of atom `O2' (compare Fig. 1 B).
This approach introduces some arbitrariness into the force computation,
because the maximum force depends on the smoothing width. To quantify that
uncertainty, we determined error bars by considering force profiles
smoothened on the scale of
ps width;
that width has been estimated from the decay of the position autocorrelation
function of atom `O2' (compare Fig. 1 B).
This approach introduces some arbitrariness into the force computation,
because the maximum force depends on the smoothing width. To quantify that
uncertainty, we determined error bars by considering force profiles
smoothened on the scale of 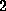 ps (providing an upper bound) and
ps (providing an upper bound) and  ps
(lower bound), respectively.
ps
(lower bound), respectively.
- 15
-
H. Frauenfelder, G. A. Petsko, D. Tsernoglou, Nature (London) 280,
558 (1979).
- 16
-
This simulation covered
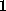 ns, within which the cantilever was moved by
ns, within which the cantilever was moved by
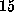 Å. Considering the structural heterogeneity mentioned above, one
cannot expect the finest details of the simulation or of the force profile to
be reproducible. Therefore, we restrict our discussion to those `typical'
features, which appeared in several of our simulations. We emphasize,
however, that many more interactions contribute to the binding forces than
those discussed here and that the rupture process is more complex than our
simplifying pictures may suggest.
Å. Considering the structural heterogeneity mentioned above, one
cannot expect the finest details of the simulation or of the force profile to
be reproducible. Therefore, we restrict our discussion to those `typical'
features, which appeared in several of our simulations. We emphasize,
however, that many more interactions contribute to the binding forces than
those discussed here and that the rupture process is more complex than our
simplifying pictures may suggest.
- 17
-
All hydrogen bonds found after equilibration are also found in the x-ray
structure [P. C. Weber et al., J. Am. Chem. Soc. 114, 3197
(1992)].
- 18
-
For subtle reasons simple integration of our force profile does not yield
correct equilibrium binding free energies. The question of whether and how
these can be obtained from our simulations is, therefore, left for future
discussion.
- 19
-
M. Eichinger, H. Grubmüller, H. Heller, User Manual for EGO_VIII,
Release 2.0, Theoretische Biophysik, Institut für Medizinische Optik,
Universität München, Theresienstr. 37, D-80333 München, Germany
(1995); electronic access: http://www.mpibpc.gwdg.de/abteilungen/071/ego.html or http://www.imo.physik.uni-muenchen.de/tavan/molgroup/moloverview.html.
- 20
-
B. R. Brooks et al., J. Comp. Chem. 4, 187 (1983).
- 21
-
A. T. Brünger, X-PLOR, The Howard Hughes Medical Institute and
Department of Molecular Biophysics and Biochemistry, Yale University, 260
Whitney Avenue, P.O. Box 6666, New Haven, CT 06511 (1988), 1992.
- 22
-
A. Kitao, F. Hirata, N. Go, J. Phys. Chem. 97, 10223
(1993).
- 23
-
W.L. Jorgenson, J. Chandrasekhar, J.D. Madura, J. Chem. Phys. 79,
927 (1983).
- 24
-
C. L. Brooks III and M. Karplus, J. Chem. Phys. 79, 6312
(1983).
- 25
-
We thank H. Gaub for stimulating this work, V. Moy for explaining details of
the AFM experiment, M. Eichinger and H. Heller for discussions and help
with the program EGO. Supported by the Deutsche Forschungsgemeinschaft,
grant SFB 143/C1.
Helmut Grubmueller
Mon Feb 12 10:15:27 MET 1996
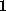 fs. The
lengths of chemical bonds involving hydrogen atoms were fixed [7],
non-polar hydrogen atoms were described through compound
atoms [20], and no explicit term for the hydrogen bond energy was
included. To quantify the strength of hydrogen bonds we used a combination of
energetic (mainly electrostatics) and steric criteria, as suggested
in [22]. The protein--ligand-complex was placed within a
sphere of TIP3 [23] water molecules with a diameter of
fs. The
lengths of chemical bonds involving hydrogen atoms were fixed [7],
non-polar hydrogen atoms were described through compound
atoms [20], and no explicit term for the hydrogen bond energy was
included. To quantify the strength of hydrogen bonds we used a combination of
energetic (mainly electrostatics) and steric criteria, as suggested
in [22]. The protein--ligand-complex was placed within a
sphere of TIP3 [23] water molecules with a diameter of 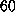 Å\
(
Å\
(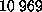 total atoms). All surface water molecules were subjected to
deformable boundary forces [24] [approximated by a quartic
polynomial [20]] and coupled to a heat bath of
total atoms). All surface water molecules were subjected to
deformable boundary forces [24] [approximated by a quartic
polynomial [20]] and coupled to a heat bath of
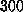 K [19] with a coupling coefficient (
K [19] with a coupling coefficient (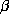 ) of
) of
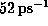 . Additionally, all atoms were weakly coupled to the heat
bath (
. Additionally, all atoms were weakly coupled to the heat
bath (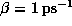 ). After minimization, the system was
equilibrated for
). After minimization, the system was
equilibrated for 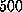 ps because it exhibited relaxations for more than
ps because it exhibited relaxations for more than
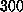 ps. After relaxation the protein backbone atoms showed a root mean
square deviation from the x-ray structure of
ps. After relaxation the protein backbone atoms showed a root mean
square deviation from the x-ray structure of 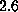 Å. Closer inspection
revealed that a large fraction of the observed deviation arose from two loops
(residues 65 to 70 and 112 to 122) at the tetramer interface, both of which
are flexible in our monomer model but fixed by intermolecular interactions in
the tetramer. The geometry of the binding pocket in our model does not
deviate significantly from that of the x-ray structure (root mean square
deviation
Å. Closer inspection
revealed that a large fraction of the observed deviation arose from two loops
(residues 65 to 70 and 112 to 122) at the tetramer interface, both of which
are flexible in our monomer model but fixed by intermolecular interactions in
the tetramer. The geometry of the binding pocket in our model does not
deviate significantly from that of the x-ray structure (root mean square
deviation 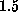 Å). Structures randomly extracted from a subsequent MD run
of
Å). Structures randomly extracted from a subsequent MD run
of 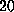 ps in duration were used for the simulations described in the text.
ps in duration were used for the simulations described in the text.
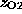 of roughly
of roughly 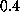 Å
, a value commonly observed for unperturbed atomic fluctuations in proteins.
Therefore, the thermal motion of the pulled atom is essentially unaffected by
the spring potential.
Å
, a value commonly observed for unperturbed atomic fluctuations in proteins.
Therefore, the thermal motion of the pulled atom is essentially unaffected by
the spring potential.
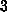 K
in the case of our slowest simulation. That heat is then effectively
transferred to the heat bath; see [11].
K
in the case of our slowest simulation. That heat is then effectively
transferred to the heat bath; see [11].
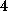 ps width;
that width has been estimated from the decay of the position autocorrelation
function of atom `O2' (compare Fig. 1 B).
This approach introduces some arbitrariness into the force computation,
because the maximum force depends on the smoothing width. To quantify that
uncertainty, we determined error bars by considering force profiles
smoothened on the scale of
ps width;
that width has been estimated from the decay of the position autocorrelation
function of atom `O2' (compare Fig. 1 B).
This approach introduces some arbitrariness into the force computation,
because the maximum force depends on the smoothing width. To quantify that
uncertainty, we determined error bars by considering force profiles
smoothened on the scale of 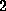 ps (providing an upper bound) and
ps (providing an upper bound) and  ps
(lower bound), respectively.
ps
(lower bound), respectively.
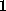 ns, within which the cantilever was moved by
ns, within which the cantilever was moved by
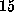 Å. Considering the structural heterogeneity mentioned above, one
cannot expect the finest details of the simulation or of the force profile to
be reproducible. Therefore, we restrict our discussion to those `typical'
features, which appeared in several of our simulations. We emphasize,
however, that many more interactions contribute to the binding forces than
those discussed here and that the rupture process is more complex than our
simplifying pictures may suggest.
Å. Considering the structural heterogeneity mentioned above, one
cannot expect the finest details of the simulation or of the force profile to
be reproducible. Therefore, we restrict our discussion to those `typical'
features, which appeared in several of our simulations. We emphasize,
however, that many more interactions contribute to the binding forces than
those discussed here and that the rupture process is more complex than our
simplifying pictures may suggest.