

Next: References
Ligand Binding:
Molecular Mechanics Calculation of the
Streptavidin-Biotin Rupture Force
Theoretische Biophysik, Institut für Medizinische Optik
Ludwig-Maximilians-Universität München
Theresienstraße 37, D-80333 München, Germany
Abstract:
The force required to rupture the streptavidin--biotin complex was
calculated here by
computer simulations. The computed force agrees well with that obtained by
recent single molecule atomic force microscope experiments.
These simulations suggest a detailed multiple-pathway rupture mechanism
involving five major unbinding steps.
Binding forces and specificity are attributed to a hydrogen bond network
between the biotin ligand and residues within the binding pocket
of streptavidin.
During rupture, additional water bridges substantially enhance the stability
of the complex and even dominate the binding interactions. In contrast,
steric restraints do not appear to contribute to the binding forces,
although conformational motions were observed.
Molecular recognition is a prerequisite for information
processing in biological systems and is
realized by specific ligand--receptor interactions.
Despite progress in obtaining experimental data on such interactions
there is little known about
the binding and unbinding reaction pathways and about the molecular basis
for the specificity of the reactions.
This lack of knowledge arises from the difficulty in bridging apparent gaps
between experimental data obtained by different techniques:
X-ray or NMR studies, on the one hand,
provide structural information at atomic resolution, but typically
yield static pictures, e.g., of
bound and unbound states. Experiments which, on the other hand,
probe the binding kinetics, rarely pertain to atomic details.

Figure 1: Experimental setups; ( A) AFM rupture experiment [1].
Biotin molecules (black ball-models) were
fixed through linker molecules to the cantilever
tip (right) as well as to an agarose bead (left).
Additionally, the biotin molecules at the cantilever were complexed with
streptavidin tetramers (only the backbone is
shown), whereas most of the biotin molecules at the bead were blocked
with soluble streptavidin. The cantilever was brought into contact with
the agarose bead, and typically only a
few streptavidin--biotin complexes were formed.
As the cantilever was subsequently retracted,
the biotin molecules were pulled out of the streptavidin binding pocket,
more or less one after
the other. Eventually one single complex remained for a
short period of time. In this case the binding force of this single
ligand--receptor pair at the point of rupture could be measured
by observation of the deflection of the cantilever.
( B) Computer simulation. One biotin molecule and one streptavidin
monomer (shown as a ribbon model) were considered.
The biotin was pulled out of the binding
pocket through a harmonic potential (the `spring'), which was moved
with constant velocity  (arrow), while the streptavidin was
kept in place. The pulling force acted on the
same biotin atom (O2), to which the linker is connected
in the AFM experiment [2].
(arrow), while the streptavidin was
kept in place. The pulling force acted on the
same biotin atom (O2), to which the linker is connected
in the AFM experiment [2].
Recent atomic force microscope (AFM) experiments
(Fig. 1 A) have probed the force required
to rupture single streptavidin--biotin complexes [1,3] and
have provided additional insights into the binding properties of
this well-known model system [4].
By measuring binding forces these AFM experiments have enabled a new view
at ligand-receptor interactions in general [1].
Conventionally, experiments on ligand binding pertain to
binding free energies; these have been calculated for the
streptavidin--biotin complex by molecular dynamics (MD)
simulations in combination with
free energy perturbation techniques [5].
However, from such calculations one cannot derive
the rupture force measured in the AFM experiments for the following
reason. The perturbation techniques mentioned above,
on the one hand, use a non-physical reaction pathway to compute
the free energy difference between bound and unbound states.
The rupture force, on the other hand, is the largest force along
the actual unbinding reaction pathway and is given
by the steepest slope in the free energy profile
along that pathway [6]. It is, therefore,
a function of the shape of the free energy profile and
generally has no relation to the value of the binding free energy.
The AFM data show that this is true for the streptavidin--biotin
complex [1].
To reveal the microscopic processes underlying the
AFM-observations we present here a theoretical approach using extended
MD simulations [7] of a large
protein-solvent system. Because of recent algorithmic and technological
advances [8], we were able to avoid nonphysical
truncations of long-range forces, which up to now have been inevitable in
simulations of that size. Our non-equilibrium approach might appear
both obvious and unusual. In our computer
simulations (Fig. 1 B) we simply
pulled the biotin out of the streptavidin
binding pocket and measured the required force --- that is,
we tried to model the AFM experiment as closely as possible [9].
As a starting point for our simulations we used the x-ray
coordinates [10]. To reduce the computational cost,
we simulated only a streptavidin monomer; we do not
expect this restriction to affect our results.
All MD simulations were carried out in water solvent [11].
As indicated by the symbolic `spring' in Fig. 1 B,
we pulled the biotin out of the binding pocket in the z-direction by
subjecting the oxygen atom O2, which in the AFM experiment was
connected to the cantilever through a linker
molecule, to a harmonic potential
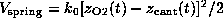 acting on
the z-coordinate
acting on
the z-coordinate
 of atom `O2'. Here,
of atom `O2'. Here,
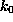 is
the spring constant and
is
the spring constant and  is
the cantilever position. This `spring'-potential,
centered at
is
the cantilever position. This `spring'-potential,
centered at  , serves
to model the elastic cantilever; accordingly,
, serves
to model the elastic cantilever; accordingly,  was shifted towards the right (positive z-direction)
with cantilever velocity
was shifted towards the right (positive z-direction)
with cantilever velocity 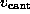 during each simulation, while the
proteins center of mass was kept in place such that the
protein was free to adjust to the pulling force by
rotational and internal motions.
Each simulation was started with
during each simulation, while the
proteins center of mass was kept in place such that the
protein was free to adjust to the pulling force by
rotational and internal motions.
Each simulation was started with  ,
such that at t=0 the `spring' was relaxed.
The spring constant
,
such that at t=0 the `spring' was relaxed.
The spring constant 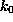 was chosen as
was chosen as
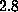 N/m [12].
As in the AFM experiment, the binding force was measured
by use of Hooke's law
by observing the deflection
N/m [12].
As in the AFM experiment, the binding force was measured
by use of Hooke's law
by observing the deflection 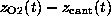 of the `cantilever' as a function of `cantilever' position
of the `cantilever' as a function of `cantilever' position
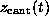 . As in the AFM experiment,
our simulated rupture force was defined as
the largest force observed during the simulated unbinding process.
. As in the AFM experiment,
our simulated rupture force was defined as
the largest force observed during the simulated unbinding process.
The only major difference between the AFM experiment and our
simulation concerns the value for the pulling velocity 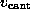 .
Whereas the experiment was carried out
on a millisecond time scale, our simulations were limited
to nanoseconds; therefore, we had to consider thermal fluctuations and
dissipation. Because of these non-equilibrium phenomena
the rupture force should vary systematically
with rupture speed [3], and thus the computed rupture forces
should be able to be extrapolated to the experimental time scale.
To do this we carried out a series of
simulations with pulling velocities
ranging from
.
Whereas the experiment was carried out
on a millisecond time scale, our simulations were limited
to nanoseconds; therefore, we had to consider thermal fluctuations and
dissipation. Because of these non-equilibrium phenomena
the rupture force should vary systematically
with rupture speed [3], and thus the computed rupture forces
should be able to be extrapolated to the experimental time scale.
To do this we carried out a series of
simulations with pulling velocities
ranging from  Å/ps down
to
Å/ps down
to 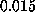 Å/ps.
The apparent linear dependency of the computed
rupture force on pulling velocity at velocities less than
Å/ps.
The apparent linear dependency of the computed
rupture force on pulling velocity at velocities less than  Å/ps
(Fig. 2) suggests that simple friction,
described by a friction coefficient of
Å/ps
(Fig. 2) suggests that simple friction,
described by a friction coefficient of 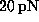 s/m,
dominates the non-equilibrium effects in this regime [13].
At velocities greater than
s/m,
dominates the non-equilibrium effects in this regime [13].
At velocities greater than 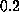 Å/ps the increase of rupture force saturates.
Å/ps the increase of rupture force saturates.
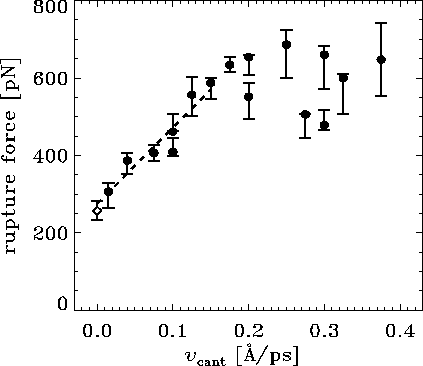
Figure: Computed rupture forces ( ) and the experimental rupture force
(
) and the experimental rupture force
( ) as a function of pulling velocity
) as a function of pulling velocity
 . For some of
the velocities two computer simulations with slightly different
initial conditions were performed.
For the computed forces,
the error bars give an estimated uncertainty [14].
The dashed line shows a linear fit to the computed forces for
values of
. For some of
the velocities two computer simulations with slightly different
initial conditions were performed.
For the computed forces,
the error bars give an estimated uncertainty [14].
The dashed line shows a linear fit to the computed forces for
values of  less than
less than
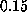 Å/ps.
Note that the experimental pulling velocity is close to 0 at the
chosen scale.
Å/ps.
Note that the experimental pulling velocity is close to 0 at the
chosen scale.
In the AFM experiment individual rupture forces scatter
considerably with a standard deviation of about 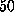 pN [1].
Of course, that scatter could be attributed exclusively to experimental error.
However, the computed rupture forces also
scatter considerably (Fig. 2),
with a standard deviation from the linear fit (for values of
pN [1].
Of course, that scatter could be attributed exclusively to experimental error.
However, the computed rupture forces also
scatter considerably (Fig. 2),
with a standard deviation from the linear fit (for values of
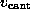 less than
less than
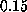 Å/ps)
of roughly
Å/ps)
of roughly  pN --- nearly as large as the observed
value of
pN --- nearly as large as the observed
value of 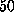 pN.
That scatter of computational results is due to a
heterogeneity of reaction pathways observed in our simulations and is related
to the known structural micro-heterogeneity of proteins commonly
described in terms of `conformational substates' [15].
pN.
That scatter of computational results is due to a
heterogeneity of reaction pathways observed in our simulations and is related
to the known structural micro-heterogeneity of proteins commonly
described in terms of `conformational substates' [15].
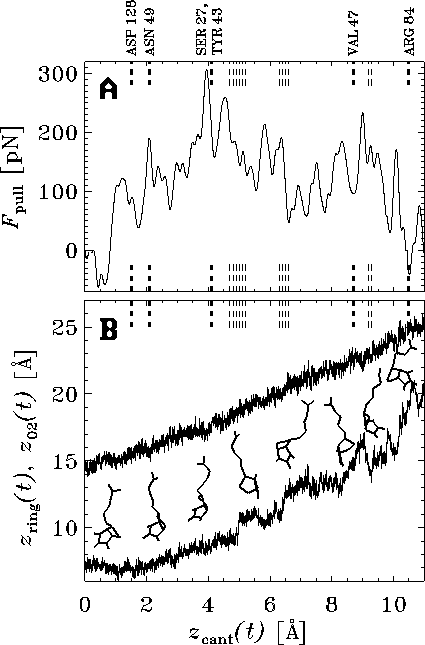
Figure: ( A) Pulling force exerted on the biotin molecule as a function
of cantilever position  at a pulling
velocity of
at a pulling
velocity of 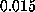 Å/ps [14].
The dashed vertical lines mark the ruptures of
hydrogen bonds (bold lines) and water bridges (thin lines)
between the biotin and the indicated residues of the
streptavidin binding pocket. ( B) `Snapshot' of the motion of the biotin.
The position of the oxygen atom O2 (see
Fig. 1 B) (upper curve),
on which the pulling force was exerted,
and the position of the center of mass of the
ureido ring (lower curve),
which points toward the interior of the binding pocket,
are plotted as a function of cantilever
position
Å/ps [14].
The dashed vertical lines mark the ruptures of
hydrogen bonds (bold lines) and water bridges (thin lines)
between the biotin and the indicated residues of the
streptavidin binding pocket. ( B) `Snapshot' of the motion of the biotin.
The position of the oxygen atom O2 (see
Fig. 1 B) (upper curve),
on which the pulling force was exerted,
and the position of the center of mass of the
ureido ring (lower curve),
which points toward the interior of the binding pocket,
are plotted as a function of cantilever
position 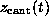 . Eight `snapshots' of the biotin
structure during rupture are depicted.
. Eight `snapshots' of the biotin
structure during rupture are depicted.
The good agreement between the results obtained in the
AFM experiment and those obtained by our
simulations enables us to suggest a detailed rupture mechanism, which we
base on the simulations with slow pulling velocities and,
in particular, the slowest one with
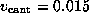 Å/ps [16].
In the force profile obtained from
this simulation (Fig. 3 A,
the apparent multitude of
force maxima mirrors the complexity of the energy landscape
traversed by the biotin on its way out of the binding pocket.
Here, the force peaks may be attributed to
the rupture of short-ranged interactions like those of hydrogen bonds.
This view is supported by the observation that
the ruptures of several dominant hydrogen bonds
and water bridges correlate well with force maxima.
Å/ps [16].
In the force profile obtained from
this simulation (Fig. 3 A,
the apparent multitude of
force maxima mirrors the complexity of the energy landscape
traversed by the biotin on its way out of the binding pocket.
Here, the force peaks may be attributed to
the rupture of short-ranged interactions like those of hydrogen bonds.
This view is supported by the observation that
the ruptures of several dominant hydrogen bonds
and water bridges correlate well with force maxima.
We obtained further insight by inspecting the motion of biotin
during rupture (Fig. 3 B).
The ureido ring moved
in a series of steps, each of which was
preceded by a force peak.
The sudden displacement of the ring at 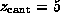 Å was
caused by rupture of apparently strong hydrogen bonds, whose preceding
elongation gave rise to the largest force peak shown
in Fig. 3 A.
By identifying this event as the experimental point
of rupture we obtained an effective
rupture length of
Å was
caused by rupture of apparently strong hydrogen bonds, whose preceding
elongation gave rise to the largest force peak shown
in Fig. 3 A.
By identifying this event as the experimental point
of rupture we obtained an effective
rupture length of 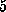 Å , which is within
the range of values estimated from the AFM experiments [1].
A second force maximum appeared at
Å , which is within
the range of values estimated from the AFM experiments [1].
A second force maximum appeared at  Å .
It was smaller than the first and has not been observed by
AFM, as only the maximum force has been able to be measured.
Å .
It was smaller than the first and has not been observed by
AFM, as only the maximum force has been able to be measured.

Figure: Snapshots of rupture. Biotin is drawn here as a ball-and-stick model
(hydrogen atoms white, heavy atoms black) within the streptavidin binding pocket;
the dashed lines show hydrogen bonds (bold) and water bridges (thin), from which
only a selection is shown. The relevant residues of the
binding pocket are drawn with depth cued lines; only polar hydrogen atoms are shown.
`Snapshots' were taken ( A) at the start of the
simulation (t=0,
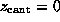 )
and after ( B)
)
and after ( B) 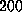 ps
(
ps
(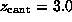 Å), ( C)
Å), ( C)
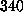 ps
(
ps
( Å),
( D)
Å),
( D)  ps
(
ps
(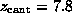 Å),
and ( E)
Å),
and ( E)  ps
(
ps
(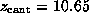 Å),
respectively [2].
Å),
respectively [2].
To explain how the measured forces arise from local interactions
between biotin and the streptavidin binding pocket,
we took a series of five `snapshots' that
characterize major steps of the rupture
process (Fig. 4).
The bound complex (Fig. 4 A) is stabilized
by a network of hydrogen bonds [17]
and a large number of water bridges between the polar
ureido ring `R' of the biotin and selected
residues of the binding pocket. The
strongest hydrogen bond (approximately  kcal/mol)
is formed to ASP 128; the combination of the
two bonds to SER 27 and
TYR 43 is of similar strength. Additionally,
the oxygen atom O2 is weakly hydrogen bonded to ASN 49.
kcal/mol)
is formed to ASP 128; the combination of the
two bonds to SER 27 and
TYR 43 is of similar strength. Additionally,
the oxygen atom O2 is weakly hydrogen bonded to ASN 49.
After the `cantilever' was moved by 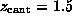 Å ,
the hydrogen bond to ASP 128 ruptured, as did subsequently
the weak bond to ASN 49 (compare the dashed lines in Fig. 3).
We were surprised to see, however, that despite a pulling force of more than
Å ,
the hydrogen bond to ASP 128 ruptured, as did subsequently
the weak bond to ASN 49 (compare the dashed lines in Fig. 3).
We were surprised to see, however, that despite a pulling force of more than
 pN this destabilization did not seem
to provoke considerable unbinding motions of the biotin
(Fig. 4 B; see also the second
snapshot in Fig. 3 B).
Rather, the particular architecture of the pocket allowed those water molecules,
which are involved in the network of water bridges,
to rearrange such as to keep the ureido ring almost in place
(for the sake of clarity, only two of the many water molecules are plotted in
Fig. 4 B).
A force larger than
pN this destabilization did not seem
to provoke considerable unbinding motions of the biotin
(Fig. 4 B; see also the second
snapshot in Fig. 3 B).
Rather, the particular architecture of the pocket allowed those water molecules,
which are involved in the network of water bridges,
to rearrange such as to keep the ureido ring almost in place
(for the sake of clarity, only two of the many water molecules are plotted in
Fig. 4 B).
A force larger than 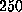 pN is required to rupture this network and the
two remaining hydrogen bonds. Only after such a force was
attained was the biotin released and
actually `flicked' forward by
pN is required to rupture this network and the
two remaining hydrogen bonds. Only after such a force was
attained was the biotin released and
actually `flicked' forward by 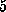 Å in two steps
(Figs. 4 C and D). This motion was
accompanied by a reorientation of the ring and by structural rearrangements
within the outer part of the binding pocket, as exemplified
by the considerable motion of ARG 84
(Figs. 4 A through D. However, because substantial
conformational motion occurs only after the force maximum, the induced
rearrangements do not seem to contribute much to the rupture force.
Å in two steps
(Figs. 4 C and D). This motion was
accompanied by a reorientation of the ring and by structural rearrangements
within the outer part of the binding pocket, as exemplified
by the considerable motion of ARG 84
(Figs. 4 A through D. However, because substantial
conformational motion occurs only after the force maximum, the induced
rearrangements do not seem to contribute much to the rupture force.
At this stage the polar ureido ring approached VAL 47 and,
after further rearrangement, formed a hydrogen bond
to this residue (Fig. 4 D,
additional water bridges are not shown).
This hydrogen bond, in combination with a subsequently established
bond to ARG 84 (Fig. 4 E) gave rise to
the second major force barrier.
The rupture process was completed only after the latter hydrogen bond broke,
which caused further deformation
of the binding pocket entry.
During the whole rupture process the biotin molecule
covered a distance as large as  Å . This total rupture length
is considerably larger than the effective rupture length
in the AFM experiment, as
the latter does not include the second force barrier.
Å . This total rupture length
is considerably larger than the effective rupture length
in the AFM experiment, as
the latter does not include the second force barrier.
Our simulations here provide detailed insight into the complex mechanisms
of streptavidin--biotin rupture. They
attribute the binding force to a network of hydrogen bonds
between the ligand and the binding pocket. In particular, the
simulations show that water bridges
actively and substantially enhance the stability of the complex.
Further work is required to also understand the energetics of the
rupture process. Upon extending our approach it should be possible to
quantify the suggested enthalpic nature [18]
of the streptavidin--biotin rupture.
Similar studies should allow the prediction of the effects of
point mutations or ligand substitutions on binding forces for various systems.
Videos
of the simulated rupture process are available.
Note added in proof: By a similar calculation of the rupture force for
iminobiotin-streptavidin we obtained 125+/-20 pN in
agreement with the AFM measurement of 135+/-15 pN (1).
A preliminary examination indicates
that the unbinding pathway differs from that for the
biotin-streptavidin system.


Next: References
Helmut Grubmueller
Mon Feb 12 10:15:27 MET 1996

 (arrow), while the streptavidin was
kept in place. The pulling force acted on the
same biotin atom (O2), to which the linker is connected
in the AFM experiment [2].
(arrow), while the streptavidin was
kept in place. The pulling force acted on the
same biotin atom (O2), to which the linker is connected
in the AFM experiment [2].

 acting on
the z-coordinate
acting on
the z-coordinate
 of atom `O2'. Here,
of atom `O2'. Here,
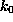 is
the spring constant and
is
the spring constant and  is
the cantilever position. This `spring'-potential,
centered at
is
the cantilever position. This `spring'-potential,
centered at  , serves
to model the elastic cantilever; accordingly,
, serves
to model the elastic cantilever; accordingly,  was shifted towards the right (positive z-direction)
with cantilever velocity
was shifted towards the right (positive z-direction)
with cantilever velocity 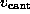 during each simulation, while the
proteins center of mass was kept in place such that the
protein was free to adjust to the pulling force by
rotational and internal motions.
Each simulation was started with
during each simulation, while the
proteins center of mass was kept in place such that the
protein was free to adjust to the pulling force by
rotational and internal motions.
Each simulation was started with  ,
such that at t=0 the `spring' was relaxed.
The spring constant
,
such that at t=0 the `spring' was relaxed.
The spring constant 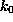 was chosen as
was chosen as
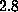 N/m [
N/m [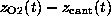 of the `cantilever' as a function of `cantilever' position
of the `cantilever' as a function of `cantilever' position
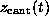 . As in the AFM experiment,
our simulated rupture force was defined as
the largest force observed during the simulated unbinding process.
. As in the AFM experiment,
our simulated rupture force was defined as
the largest force observed during the simulated unbinding process.
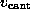 .
Whereas the experiment was carried out
on a millisecond time scale, our simulations were limited
to nanoseconds; therefore, we had to consider thermal fluctuations and
dissipation. Because of these non-equilibrium phenomena
the rupture force should vary systematically
with rupture speed [
.
Whereas the experiment was carried out
on a millisecond time scale, our simulations were limited
to nanoseconds; therefore, we had to consider thermal fluctuations and
dissipation. Because of these non-equilibrium phenomena
the rupture force should vary systematically
with rupture speed [ Å/ps down
to
Å/ps down
to 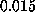 Å/ps.
The apparent linear dependency of the computed
rupture force on pulling velocity at velocities less than
Å/ps.
The apparent linear dependency of the computed
rupture force on pulling velocity at velocities less than  Å/ps
(Fig.
Å/ps
(Fig. 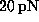 s/m,
dominates the non-equilibrium effects in this regime [
s/m,
dominates the non-equilibrium effects in this regime [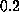 Å/ps the increase of rupture force saturates.
Å/ps the increase of rupture force saturates.

 ) and the experimental rupture force
(
) and the experimental rupture force
(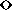 ) as a function of pulling velocity
) as a function of pulling velocity
 . For some of
the velocities two computer simulations with slightly different
initial conditions were performed.
For the computed forces,
the error bars give an estimated uncertainty [
. For some of
the velocities two computer simulations with slightly different
initial conditions were performed.
For the computed forces,
the error bars give an estimated uncertainty [ less than
less than
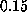 Å/ps.
Note that the experimental pulling velocity is close to 0 at the
chosen scale.
Å/ps.
Note that the experimental pulling velocity is close to 0 at the
chosen scale.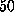 pN [
pN [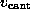 less than
less than
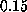 Å/ps)
of roughly
Å/ps)
of roughly  pN --- nearly as large as the observed
value of
pN --- nearly as large as the observed
value of 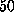 pN.
That scatter of computational results is due to a
heterogeneity of reaction pathways observed in our simulations and is related
to the known structural micro-heterogeneity of proteins commonly
described in terms of `conformational substates' [
pN.
That scatter of computational results is due to a
heterogeneity of reaction pathways observed in our simulations and is related
to the known structural micro-heterogeneity of proteins commonly
described in terms of `conformational substates' [
 at a pulling
velocity of
at a pulling
velocity of 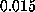 Å/ps [
Å/ps [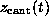 . Eight `snapshots' of the biotin
structure during rupture are depicted.
. Eight `snapshots' of the biotin
structure during rupture are depicted.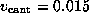 Å/ps [
Å/ps [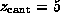 Å was
caused by rupture of apparently strong hydrogen bonds, whose preceding
elongation gave rise to the largest force peak shown
in Fig.
Å was
caused by rupture of apparently strong hydrogen bonds, whose preceding
elongation gave rise to the largest force peak shown
in Fig. 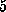 Å , which is within
the range of values estimated from the AFM experiments [
Å , which is within
the range of values estimated from the AFM experiments [ Å .
It was smaller than the first and has not been observed by
AFM, as only the maximum force has been able to be measured.
Å .
It was smaller than the first and has not been observed by
AFM, as only the maximum force has been able to be measured.

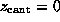 )
and after ( B)
)
and after ( B) 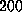 ps
(
ps
(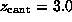 Å), ( C)
Å), ( C)
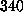 ps
(
ps
( Å),
( D)
Å),
( D)  ps
(
ps
(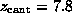 Å),
and ( E)
Å),
and ( E)  ps
(
ps
(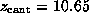 Å),
respectively [
Å),
respectively [ kcal/mol)
is formed to ASP 128; the combination of the
two bonds to SER 27 and
TYR 43 is of similar strength. Additionally,
the oxygen atom O2 is weakly hydrogen bonded to ASN 49.
kcal/mol)
is formed to ASP 128; the combination of the
two bonds to SER 27 and
TYR 43 is of similar strength. Additionally,
the oxygen atom O2 is weakly hydrogen bonded to ASN 49.
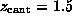 Å ,
the hydrogen bond to ASP 128 ruptured, as did subsequently
the weak bond to ASN 49 (compare the dashed lines in Fig.
Å ,
the hydrogen bond to ASP 128 ruptured, as did subsequently
the weak bond to ASN 49 (compare the dashed lines in Fig.  pN this destabilization did not seem
to provoke considerable unbinding motions of the biotin
(Fig.
pN this destabilization did not seem
to provoke considerable unbinding motions of the biotin
(Fig. 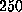 pN is required to rupture this network and the
two remaining hydrogen bonds. Only after such a force was
attained was the biotin released and
actually `flicked' forward by
pN is required to rupture this network and the
two remaining hydrogen bonds. Only after such a force was
attained was the biotin released and
actually `flicked' forward by 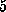 Å in two steps
(Figs.
Å in two steps
(Figs.  Å . This total rupture length
is considerably larger than the effective rupture length
in the AFM experiment, as
the latter does not include the second force barrier.
Å . This total rupture length
is considerably larger than the effective rupture length
in the AFM experiment, as
the latter does not include the second force barrier.